题目内容
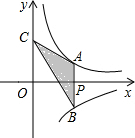 如图,过x轴正半轴上的任意一点P作y轴的平行线交反比例函数y=
如图,过x轴正半轴上的任意一点P作y轴的平行线交反比例函数y=| 2 |
| x |
| 4 |
| x |
考点:反比例函数系数k的几何意义
专题:
分析:设P(a,0),由直线APB与y轴平行,得到A和B的横坐标都为a,将x=a代入反比例函数y=
和y=-
中,分别表示出A和B的纵坐标,进而由AP+BP表示出AB,三角形ABC的面积=
×AB×OP,求出即可.
| 2 |
| x |
| 4 |
| x |
| 1 |
| 2 |
解答:解:设P(a,0),a>0,则A和B的横坐标都为a,
将x=a代入反比例函数y=
中得:y=
,故A(a,
);
将x=a代入反比例函数y=-
中得:y=-
,故B(a,-
),
∴AB=AP+BP=
+
=
,
则S△ABC=
AB•OP=
×
×a=3.
故答案为3.
将x=a代入反比例函数y=
| 2 |
| x |
| 2 |
| a |
| 2 |
| a |
将x=a代入反比例函数y=-
| 4 |
| x |
| 4 |
| a |
| 4 |
| a |
∴AB=AP+BP=
| 2 |
| a |
| 4 |
| a |
| 6 |
| a |
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| a |
故答案为3.
点评:此题考查了反比例函数系数k的几何意义,以及坐标与图形性质,其中设出P的坐标,表示出AB是解本题的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 如图,AB∥CD,
如图,AB∥CD, 如图,在△ABC中,∠A=55°,b=20cm,c=30cm,求S△ABC(参考数据:sin55°≈0.8192,结果精确到0.1cm2)
如图,在△ABC中,∠A=55°,b=20cm,c=30cm,求S△ABC(参考数据:sin55°≈0.8192,结果精确到0.1cm2)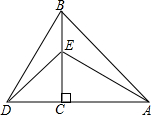 如图,△ACB与△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在BC上,连接AE,BD.
如图,△ACB与△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点E在BC上,连接AE,BD. 如图,AB是⊙O直径,∠AOC=130°,则∠D=
如图,AB是⊙O直径,∠AOC=130°,则∠D= 如图,直线AB,CD相交于点O,EO⊥CD于点O,FO⊥AB于点O,∠DOF=65°,求∠BOE的度数.
如图,直线AB,CD相交于点O,EO⊥CD于点O,FO⊥AB于点O,∠DOF=65°,求∠BOE的度数.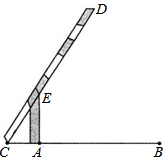 如图,小明在研究性学习活动中,对自己家所在的小区进行调查后发现,小区汽车入口宽AB为3.2m,在入口的一侧安装了停止杆CD,其中AE为支架.当停止杆仰起并与地面成60°角时,停止杆的端点C恰好与地面接触.此时CA为0.7m.在此状态下,若一辆货车高3m,宽2.5m,入口两侧不能通车,那么这辆货车在不碰杆的情况下,能从入口内通过吗?请你通过估算说明.(参考数据:
如图,小明在研究性学习活动中,对自己家所在的小区进行调查后发现,小区汽车入口宽AB为3.2m,在入口的一侧安装了停止杆CD,其中AE为支架.当停止杆仰起并与地面成60°角时,停止杆的端点C恰好与地面接触.此时CA为0.7m.在此状态下,若一辆货车高3m,宽2.5m,入口两侧不能通车,那么这辆货车在不碰杆的情况下,能从入口内通过吗?请你通过估算说明.(参考数据: 如图,机器人从A点出发,沿着西南方向行了4
如图,机器人从A点出发,沿着西南方向行了4