题目内容
已知∠ACD=90°,MN是过点A的直线,AC=DC,且DB⊥MN于点B,如图(1).易证BD+AB=
CB,过程如下:
解:过点C作CE⊥CB于点C,与MN交于点E
∵∠ACB+∠BCD=90°,∠ACB+∠ACE=90°,
∴∠BCD=∠ACE.
∵DB⊥MN∴∠ABC+∠CBD=90°,
∵CE⊥CB∴∠ABC+∠CEA=90°,
∴∠CBD=∠CEA.
又∵AC=DC,
∴△ACE≌△DCB(AAS),
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=
CB.
又∵BE=AE+AB,∴BE=BD+AB,
∴BD+AB=
CB.
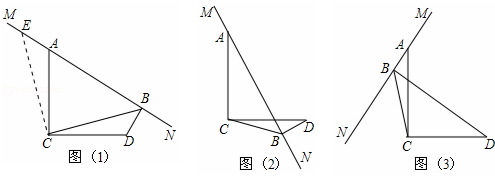
(1)当MN绕A旋转到如图(2)位置时,BD、AB、CB满足什么样关系式,请写出你的猜想,并给予证明.
(2)当MN绕A旋转到如图(3)位置时,BD、AB、CB满足什么样关系式,请直接写出你的结论.
| 2 |
解:过点C作CE⊥CB于点C,与MN交于点E
∵∠ACB+∠BCD=90°,∠ACB+∠ACE=90°,
∴∠BCD=∠ACE.
∵DB⊥MN∴∠ABC+∠CBD=90°,
∵CE⊥CB∴∠ABC+∠CEA=90°,
∴∠CBD=∠CEA.
又∵AC=DC,
∴△ACE≌△DCB(AAS),
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=
| 2 |
又∵BE=AE+AB,∴BE=BD+AB,
∴BD+AB=
| 2 |

(1)当MN绕A旋转到如图(2)位置时,BD、AB、CB满足什么样关系式,请写出你的猜想,并给予证明.
(2)当MN绕A旋转到如图(3)位置时,BD、AB、CB满足什么样关系式,请直接写出你的结论.
考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)仿照图(1)的解题过程即可解答.过点C作CE⊥CB于点C,与MN交于点E,根据同角(等角)的余角相等可证∠BCD=∠ACE及∠CAE=∠D,由ASA可证△ACE≌△DCB,然后由全等三角形的对应边相等可得:AE=DB,CE=CB,从而确定△ECB为等腰直角三角形,由勾股定理可得:BE=
CB,由BE=AB-AE,可得BE=AB-BD,即AB-BD=
CB;
(2)解题思路同(1),过点C作CE⊥CB于点C,与MN交于点E,根据等角的余角相等及等式的性质可证∠BCD=∠ACE及∠CAE=∠D,由ASA可证△ACE≌△DCB,然后由全等三角形的对应边相等可得:AE=DB,CE=CB,从而确定△ECB为等腰直角三角形,由勾股定理可得:BE=
CB,由BE=AE-AB,可得BE=BD-AB,即BD-AB=
CB.
| 2 |
| 2 |
(2)解题思路同(1),过点C作CE⊥CB于点C,与MN交于点E,根据等角的余角相等及等式的性质可证∠BCD=∠ACE及∠CAE=∠D,由ASA可证△ACE≌△DCB,然后由全等三角形的对应边相等可得:AE=DB,CE=CB,从而确定△ECB为等腰直角三角形,由勾股定理可得:BE=
| 2 |
| 2 |
解答:(1)AB-BD=
CB.
证明:如图(2)过点C作CE⊥CB于点C,与MN交于点E,

∵∠ACD=90°,∠ECB=90°,
∴∠ACE=90°-∠DCE,∠BCD=90°-∠ECD,
∴∠BCD=∠ACE.
∵DB⊥MN,
∴∠CAE=90°-∠AFC,∠D=90°-∠BFD,
∵∠AFC=∠BFD,
∴∠CAE=∠D,
在△ACE和△DCB中,
∴△ACE≌△DCB(ASA),
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=
CB.
又∵BE=AB-AE,
∴BE=AB-BD,
∴AB-BD=
CB.
(2)BD-AB=
CB.
如图(3)过点C作CE⊥CB于点C,与MN交于点E,

∵∠ACD=90°,∠BCE=90°,
∴∠ACE=90°+∠ACB,∠BCD=90°+∠ACB,
∴∠BCD=∠ACE.
∵DB⊥MN,
∴∠CAE=90°-∠AFC,∠D=90°-∠BFD,
∵∠AFC=∠BFD,
∴∠CAE=∠D,
在△ACE和△DCB中,
∴△ACE≌△DCB(ASA),
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=
CB.
又∵BE=AE-AB,
∴BE=BD-AB,
∴BD-AB=
CB.
| 2 |
证明:如图(2)过点C作CE⊥CB于点C,与MN交于点E,

∵∠ACD=90°,∠ECB=90°,
∴∠ACE=90°-∠DCE,∠BCD=90°-∠ECD,
∴∠BCD=∠ACE.
∵DB⊥MN,
∴∠CAE=90°-∠AFC,∠D=90°-∠BFD,
∵∠AFC=∠BFD,
∴∠CAE=∠D,
在△ACE和△DCB中,
|
∴△ACE≌△DCB(ASA),
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=
| 2 |
又∵BE=AB-AE,
∴BE=AB-BD,
∴AB-BD=
| 2 |
(2)BD-AB=
| 2 |
如图(3)过点C作CE⊥CB于点C,与MN交于点E,

∵∠ACD=90°,∠BCE=90°,
∴∠ACE=90°+∠ACB,∠BCD=90°+∠ACB,
∴∠BCD=∠ACE.
∵DB⊥MN,
∴∠CAE=90°-∠AFC,∠D=90°-∠BFD,
∵∠AFC=∠BFD,
∴∠CAE=∠D,
在△ACE和△DCB中,
|
∴△ACE≌△DCB(ASA),
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=
| 2 |
又∵BE=AE-AB,
∴BE=BD-AB,
∴BD-AB=
| 2 |
点评:本题考查了三角形全等的判定和性质,等腰直角三角形的判定和性质等.注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的性质是全等三角形的对应边相等,对应角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在△ABC中,∠A=55°,b=20cm,c=30cm,求S△ABC(参考数据:sin55°≈0.8192,结果精确到0.1cm2)
如图,在△ABC中,∠A=55°,b=20cm,c=30cm,求S△ABC(参考数据:sin55°≈0.8192,结果精确到0.1cm2)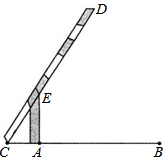 如图,小明在研究性学习活动中,对自己家所在的小区进行调查后发现,小区汽车入口宽AB为3.2m,在入口的一侧安装了停止杆CD,其中AE为支架.当停止杆仰起并与地面成60°角时,停止杆的端点C恰好与地面接触.此时CA为0.7m.在此状态下,若一辆货车高3m,宽2.5m,入口两侧不能通车,那么这辆货车在不碰杆的情况下,能从入口内通过吗?请你通过估算说明.(参考数据:
如图,小明在研究性学习活动中,对自己家所在的小区进行调查后发现,小区汽车入口宽AB为3.2m,在入口的一侧安装了停止杆CD,其中AE为支架.当停止杆仰起并与地面成60°角时,停止杆的端点C恰好与地面接触.此时CA为0.7m.在此状态下,若一辆货车高3m,宽2.5m,入口两侧不能通车,那么这辆货车在不碰杆的情况下,能从入口内通过吗?请你通过估算说明.(参考数据: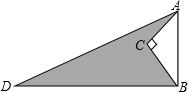 如图,AD=13,BD=12,∠C=90°,AC=3,BC=4.则阴影部分的面积=
如图,AD=13,BD=12,∠C=90°,AC=3,BC=4.则阴影部分的面积=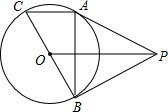 如图,P为⊙O外一点,PA、PB均为⊙O的切线,A和B是切点,BC是直径.求证:
如图,P为⊙O外一点,PA、PB均为⊙O的切线,A和B是切点,BC是直径.求证:
 如图,机器人从A点出发,沿着西南方向行了4
如图,机器人从A点出发,沿着西南方向行了4 如图,在Rt△ABC中,∠A=90°,AB=1,BC=2,∠ACB的平分线CD交AB于点D,则
如图,在Rt△ABC中,∠A=90°,AB=1,BC=2,∠ACB的平分线CD交AB于点D,则