题目内容
2.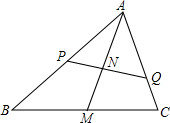 设AM是△ABC中BC边上的中线,任作一条直线分别交AB,AC,AM于P,Q,N,求证:$\frac{2AM}{AN}$=$\frac{AB}{AP}$+$\frac{AC}{AQ}$.
设AM是△ABC中BC边上的中线,任作一条直线分别交AB,AC,AM于P,Q,N,求证:$\frac{2AM}{AN}$=$\frac{AB}{AP}$+$\frac{AC}{AQ}$.
分析 过B作BD∥PQ,过C作CE∥PQ,分别交直线AM于D、E,得到BD∥CE,根据平行线的性质得到∠BDM=∠CEM,推出△BDM≌△CEM(AAS),根据全等三角形的性质得到MD=ME,根据平行线分线段成比例得到∴$\frac{AB}{AP}=\frac{AD}{AN}$,$\frac{AC}{AQ}=\frac{AE}{AN}$,于是得到$\frac{AB}{AP}+\frac{AC}{AQ}=\frac{AE+AD}{AN}$,根据线段的和差得到AE=AM+ME,AD=AM-MD,于是得到结论.
解答 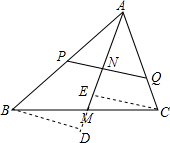 证明:过B作BD∥PQ,过C作CE∥PQ,分别交直线AM于D、E,
证明:过B作BD∥PQ,过C作CE∥PQ,分别交直线AM于D、E,
∴BD∥CE,
∴∠BDM=∠CEM,在△BDM与△CEM中,$\left\{\begin{array}{l}{∠BDM=∠CEM}\\{DM=EM}\\{∠BMD=∠CME}\end{array}\right.$,
∴△BDM≌△CEM(AAS),
∴MD=ME,
∵PQ∥BD,PQ∥CE
∴$\frac{AB}{AP}=\frac{AD}{AN}$,$\frac{AC}{AQ}=\frac{AE}{AN}$,
∴$\frac{AB}{AP}+\frac{AC}{AQ}=\frac{AE+AD}{AN}$,
∵AE=AM+ME,AD=AM-MD
∴AE+AD=2AM
∴$\frac{2AM}{AN}$=$\frac{AB}{AP}$+$\frac{AC}{AQ}$.
点评 本题考查了平行线分线段成比例定理,全等三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
12.市场调查显示,每年深圳体育中考前几个月,某种品牌的跑鞋将会热销.某公司为了抓住这一商机,决定进一批这种品牌的跑鞋,该公司对某中学初三学生的鞋码进行了调查,你认为该公司最关注的是这一组鞋码的( )
| A. | 中位数 | B. | 平均数 | C. | 众数 | D. | 加权平均数 |
13. 美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感,如图,某女士身高165cm,下半身长x与身高L的比值为0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )
美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感,如图,某女士身高165cm,下半身长x与身高L的比值为0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )
 美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感,如图,某女士身高165cm,下半身长x与身高L的比值为0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )
美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感,如图,某女士身高165cm,下半身长x与身高L的比值为0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )| A. | 10cm | B. | 7.8cm | C. | 6.5cm | D. | 5cm |
14.三角形的两边分别为5和6,第三边长是方程x2-6x+8=0的解,则这个三角形的周长是( )
| A. | 13 | B. | 15 | C. | 13或15 | D. | 13和15 |
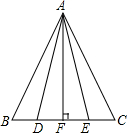 在△ABC中,AB=AC,AF⊥BC,BD=CE,则图中全等三角形共有4对.
在△ABC中,AB=AC,AF⊥BC,BD=CE,则图中全等三角形共有4对.