题目内容
12.解不等式(组)(1)2(x-5)+1>x-3
(2)$\left\{{\begin{array}{l}{x-3(x-2)<4}\\{\frac{1-2x}{4}<1-x}\end{array}}\right.$.
分析 (1)去括号整理后,应把含x的项移到不等号的左边,移项及合并即可.
(2)分别求出各不等式的解集,再求出其公共解即可.
解答 解;(1)2(x-5)+1>x-3
去括号得,2x-10+1>x-3,
移项及合并得,x>6.
(2)$\left\{\begin{array}{l}{x-3(x-2)<4①}\\{\frac{1-2x}{4}<1-x②}\end{array}\right.$
由①得,x>1;
由②得,x<1.5,
所以,不等式组的解集是1<x<1.5.
点评 本题考查了解一元一次不等式(组),熟练掌握不等式的性质是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
3.某市商品房的均价原为18150元/m2,经过连续两次降价后均价为15000元/m2.设平均每次降价的百分率为x,根据题意所列方程正确的是( )
| A. | 18150(1-x)2=18150-15000 | B. | 18150(1-x2)=15000 | ||
| C. | 18150(1-2x)=15000 | D. | 18150(1-x)2=15000 |
7.已知方程组$\left\{\begin{array}{l}2x+y=2-5a\\ x-2y=3a\end{array}\right.$的解x,y的和是负数,满足条件的最小整数a是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
1.点A(x1,y1)、B(x2,y2)、C(x3,y3)都在反比例函数y=-$\frac{4}{x}$的图象上,且x1<0<x2<x3,则y1、y2、y3的大小关系是( )
| A. | y3<y1<y2 | B. | y1<y2<y3 | C. | y3<y2<y1 | D. | y2<y3<y1 |
2.甲数为x,乙数为y,则甲数的3倍与乙数的和除甲数与乙数的3倍的差,可表示为( )
| A. | $\frac{3x+y}{x-3y}$ | B. | $\frac{3x-y}{x+3y}$ | C. | $\frac{x-3y}{3x+y}$ | D. | $\frac{x+3y}{3x-y}$ |
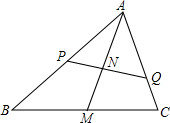 设AM是△ABC中BC边上的中线,任作一条直线分别交AB,AC,AM于P,Q,N,求证:$\frac{2AM}{AN}$=$\frac{AB}{AP}$+$\frac{AC}{AQ}$.
设AM是△ABC中BC边上的中线,任作一条直线分别交AB,AC,AM于P,Q,N,求证:$\frac{2AM}{AN}$=$\frac{AB}{AP}$+$\frac{AC}{AQ}$.