题目内容
14.三角形的两边分别为5和6,第三边长是方程x2-6x+8=0的解,则这个三角形的周长是( )| A. | 13 | B. | 15 | C. | 13或15 | D. | 13和15 |
分析 求出已知方程的解确定出第三边,即可求出三角形周长.
解答 解:方程x2-6x+8=0,
分解因式得:(x-4)(x-2)=0,
解得:x1=4,x2=2,
当x=4时,三角形三边长为4,5,6,能构成三角形,周长为4+5+6=15;
当x=2时,三角形三边长为2,5,6,能构成三角形,周长为2+5+6=13,
故选:C.
点评 此题考查了解一元二次方程-因式分解法,以及三角形三边关系,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.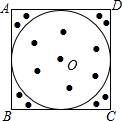 正方形ABCD内,有一个内切圆⊙O.电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数a个,⊙O内的点数b个(在正方形边上和圆上的点不在统计中),根据用频率估计概率的原理,可推得π的大小是( )
正方形ABCD内,有一个内切圆⊙O.电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数a个,⊙O内的点数b个(在正方形边上和圆上的点不在统计中),根据用频率估计概率的原理,可推得π的大小是( )
 正方形ABCD内,有一个内切圆⊙O.电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数a个,⊙O内的点数b个(在正方形边上和圆上的点不在统计中),根据用频率估计概率的原理,可推得π的大小是( )
正方形ABCD内,有一个内切圆⊙O.电脑可设计程序:在正方形内可随机产生一系列点,当点数很多时,电脑自动统计正方形内的点数a个,⊙O内的点数b个(在正方形边上和圆上的点不在统计中),根据用频率估计概率的原理,可推得π的大小是( )| A. | π≈$\frac{a}{b}$ | B. | π≈$\frac{4b}{a}$ | C. | π≈$\frac{b}{a}$ | D. | π≈$\frac{4a}{b}$ |
3.某市商品房的均价原为18150元/m2,经过连续两次降价后均价为15000元/m2.设平均每次降价的百分率为x,根据题意所列方程正确的是( )
| A. | 18150(1-x)2=18150-15000 | B. | 18150(1-x2)=15000 | ||
| C. | 18150(1-2x)=15000 | D. | 18150(1-x)2=15000 |
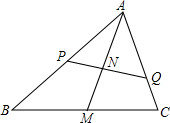 设AM是△ABC中BC边上的中线,任作一条直线分别交AB,AC,AM于P,Q,N,求证:$\frac{2AM}{AN}$=$\frac{AB}{AP}$+$\frac{AC}{AQ}$.
设AM是△ABC中BC边上的中线,任作一条直线分别交AB,AC,AM于P,Q,N,求证:$\frac{2AM}{AN}$=$\frac{AB}{AP}$+$\frac{AC}{AQ}$.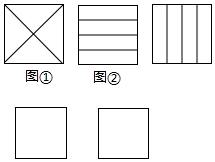 一块正方形空地按下列要求分成四块:(1)被画分割线后整个图形仍是轴对称图形;(2)四个图形形状相同;(3)四个图形面积相等.
一块正方形空地按下列要求分成四块:(1)被画分割线后整个图形仍是轴对称图形;(2)四个图形形状相同;(3)四个图形面积相等. 已知,如图,△ABC中,∠A=90°,AB=AC,D是BC边上的中点,E、F分别是AB、AC上的点,且∠EDF=90°,求证:BE=AF.
已知,如图,△ABC中,∠A=90°,AB=AC,D是BC边上的中点,E、F分别是AB、AC上的点,且∠EDF=90°,求证:BE=AF.