题目内容
11.如图1,正方形ABCD中,点E是CD的延长线上一点,将△ADE沿AE对折至△AFE,FE的延长线与BC的延长线交于点G,连接AG.(1)求证:AG平分∠FAB;
(2)如图2,GB的延长线交FA的延长线于点H,试探究线段DE、AH、BH三者之间的数量关系;
(3)在(2)的条件填空:∠GAE=45°度;若DC=2DE,则$\frac{BH}{CG}$=$\frac{3}{8}$.

分析 (1)根据角平分线的判定定理即可判定.
(2)如图2中,将△ADE绕点A顺时针旋转90°得到△ABM,只要证明∠HAM=∠AMH即可得到AH=HM由此即可解决问题.
(3)如图2中,①只要证明△AGE≌△AGM即可,②设正方形ABCD边长为2a,则CE=3a,BM=DE=a,AM=$\sqrt{A{B}^{2}+B{M}^{2}}$=$\sqrt{5}$a,设AH=HM=x,在RT△AHB中利用勾股定理求出x与a的关系,再利用△ABH∽△GCE得$\frac{AB}{CG}$=$\frac{HB}{EC}$求出CG即可解决问题.
解答 (1)证明: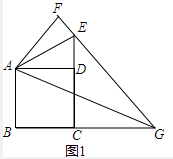 ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AD=AB,∠B=∠ADC=∠ADE=90°,
∵△AEF是由△AED翻折得到,
∴AF=AD,∠F=∠ADE=90°,
∴AF⊥CF,AB⊥BG,AF=AB,
∴AG平分∠BGF.
(2)如图2中,将△ADE绕点A顺时针旋转90°得到△ABM,
∵∠ADE=∠ABM=90°,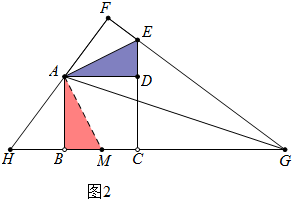
∴点M在线段BC上,DE=BM,
∵∠EAM=90°,
∴∠EAF+∠HAM=90°,
∵∠EAD+∠DAM=90°,
∴∠HAM=∠DAM,
∵AD∥BC,
∴∠DAM=∠AMH,
∴∠HAM=∠AMH,
∴AH=HM=BH+BM=BH+DE.
(3)①如图2中,在△AGF和△AGB中,
$\left\{\begin{array}{l}{∠AGF=∠AGB}\\{∠F=∠ABC=90°}\\{AG=AG}\end{array}\right.$,
∴△AGF≌△AGB,
∴GF=GB,
∵EF=ED=BM,
∴GE=GM,
在△AGE和△AGM中,
$\left\{\begin{array}{l}{AG=AG}\\{GE=GM}\\{AE=AM}\end{array}\right.$,
∴△AGE≌△AGM,
∴∠GAE=∠GAM=45°
②设正方形ABCD边长为2a,则CE=3a,BM=DE=a,AM=$\sqrt{A{B}^{2}+B{M}^{2}}$=$\sqrt{5}$a,设AH=HM=x,
在RT△AHB中,∵AH2=AB2+HB2,
∴x2=4a2+(x-a)2,
∴x=$\frac{5}{2}$a,
∴BH=$\frac{3}{2}$a,
∵∠HAB+∠FAB=180°,∠FAB+∠EGC=180°,
∴∠HAB=∠EGC,
∵∠ABH=∠ECG=90°,
∴△ABH∽△GCE,
∴$\frac{AB}{CG}$=$\frac{HB}{EC}$,
∴$\frac{2a}{CG}$=$\frac{\frac{3}{2}a}{3a}$,
∴CG=4a,
∴$\frac{BH}{CG}$=$\frac{\frac{3}{2}a}{4a}$=$\frac{3}{8}$.
故答案分别为45°,$\frac{3}{8}$.
点评 本题考查四边形综合题、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是利用旋转添加辅助线构造全等三角形,最后一个填空比较难,需要学会设参数解决问题,属于中考压轴题.

| A. | 一组边对应相等 | B. | 两组直角边对应相等 | ||
| C. | 两组锐角对应相等 | D. | 一组锐角对应相等 |
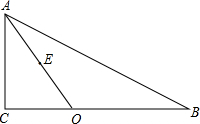 如图,在Rt△ABC中,∠C=90°,AC=4,O是BC上一点,且OC=3,E是AO的中点,如以O为圆心,OC为半径作圆,求点E和⊙O的位置关系.
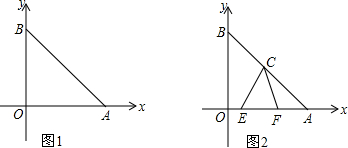
如图,在Rt△ABC中,∠C=90°,AC=4,O是BC上一点,且OC=3,E是AO的中点,如以O为圆心,OC为半径作圆,求点E和⊙O的位置关系.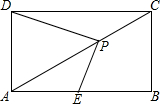 如图,在长方形ABCD中,AB=2$\sqrt{3}$,AC=4,E点为AB的中点,点P为对角线AC上的一动点.则①BC=2;②PD+PE的最小值等于$\sqrt{7}$.
如图,在长方形ABCD中,AB=2$\sqrt{3}$,AC=4,E点为AB的中点,点P为对角线AC上的一动点.则①BC=2;②PD+PE的最小值等于$\sqrt{7}$.