题目内容
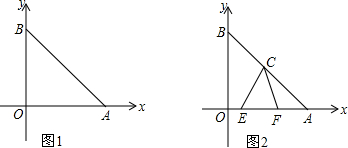
6.已知点A、B分别在x轴,y轴上,OA=OB,点C为AB的中点,AB=12$\sqrt{2}$(1)如图1,求点C的坐标;
(2)如图2,E、F分别为OA上的动点,且∠ECF=45°,求证:EF2=OE2+AF2;
(3)在条件(2)中,若点E的坐标为(3,0),求CF的长.
分析 (1)连接OC,作CM⊥OA于点M,由等腰直角三角形的性质可以得出CM=OM=$\frac{1}{2}$OA=$\frac{\sqrt{2}}{4}$AB,结合AB的长度即可得出点C的坐标;
(2)连接OC,在OB上截取OM=AF,连接CM、ME.通过证明△ACF≌△OCM得出“CM=CF,∠OCM=∠ACF”,再通过角的计算得出∠ECM=∠ECF=45°,从而△ECF与△ECM满足全等三角形的判定定理(SAS),即得出ME=EF,在Rt△MOE中,通过勾股定理即可得出结论;
(3)过点C作CN⊥OA于点N.设AF=x=OM,则EF=9-x=EM,在Rt△MOE中由勾股定理即可得出关于x的一元二次方程,解方程即可得出x的值,再由等腰直角三角形的性质可得出CN、NF的长,在Rt△CNF中结合勾股定理即可得出结论.
解答 解:(1)连接OC,作CM⊥OA于点M,如图1所示.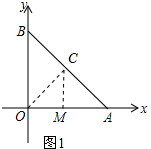
∵OA=OB,∠AOB=90°,
∴△AOB为等腰直角三角形,
∴OA=OB=12.
∵点C为线段AB的中点,
∴OC⊥AB,
∴△OCA为等腰直角三角形,
又∵CM⊥OA,
∴CM=OM=MA=$\frac{1}{2}$OA=6.
故点C的坐标为(6,6).
(2)证明:连接OC,在OB上截取OM=AF,连接CM、ME,如图2所示.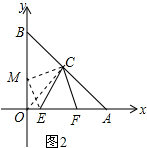
∵△AOB、△OCA、△OCB均为等腰直角三角形,
∴∠A=∠B=∠BOC=45°,OC=AC.
在△ACF和△OCM中,
$\left\{\begin{array}{l}{OM=AF}\\{∠A=∠MOC}\\{OC=AC}\end{array}\right.$,
∴△ACF≌△OCM(SAS),
∴CM=CF,∠OCM=∠ACF.
∵∠ACO=∠ACF+∠ECF+∠OCE=90°,∠ECF=45°,
∴∠ACF+∠OCE=45°=∠OCM+∠OCE=∠ECM=∠ECF.
在△ECF和△ECM中,
$\left\{\begin{array}{l}{EC=EC}\\{∠ECM=∠ECF=45°}\\{CM=CF}\end{array}\right.$,
∴△ECF≌△ECM(SAS),
∴ME=EF.
在Rt△MOE中,∠MOE=90°,
∴EF2=ME2=OE2+OM2=OE2+AF2.
(3)过点C作CN⊥OA于点N,如图3所示.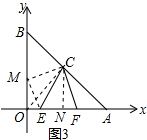
设AF=x=OM,则EF=OA-OE-AF=12-3-x=9-x=EM,
由(2)可得:(9-x)2=32+x2,
解得:x=4,
∴OF=OA-AF=12-4=8.
∵△OCA为等腰直角三角形,
∴CN=ON=$\frac{1}{2}$OA=6,NF=OF-ON=8-6=2.
在Rt△CNF中,∠CNF=90°,CN=6,NF=2,
∴CF=$\sqrt{C{N}^{2}+N{F}^{2}}$=2$\sqrt{10}$.
点评 本题考查了等腰直角三角形的性质、全等三角形的判定及性质、角的计算以及勾股定理,解题的关键:(1)由等腰直角三角形的性质找出CM=OM=6;(2)根据全等三角形的性质找出ME=EF;(3)求出CN=6、NF=2.本题属于基础题,难度不大,解决该题型题目时,通过角的计算找出相等的角,再结合全等三角形的判定定理证出三角形全等是关键.

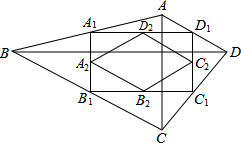 如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,如此进行下去,得到四边形AnBnCnDn.
如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1,再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2,如此进行下去,得到四边形AnBnCnDn.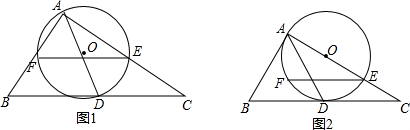

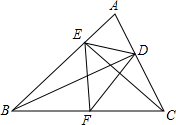 如图,在锐角△ABC中,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①DE=EF;②AD:AB=AE:AC;③△AEC∽△ADB;④AE+AD=BC,其中正确结论的序号是②③(写上所有正确结论的序号)
如图,在锐角△ABC中,BD、CE为高,F为BC的中点,连接DE、DF、EF,则结论:①DE=EF;②AD:AB=AE:AC;③△AEC∽△ADB;④AE+AD=BC,其中正确结论的序号是②③(写上所有正确结论的序号)