Question

3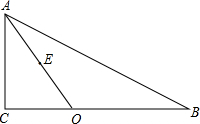．如图，在Rt△ABC中，∠C=90°，AC=4，O是BC上一点，且OC=3，E是AO的中点，如以O为圆心，OC为半径作圆，求点E和⊙O的位置关系．

Answer 1

分析 在Rt△ACO中，由勾股定理可求出OA的长度，由中点的定义可得出OE的长度，再将OE、OC进行比较，由OE＜OC可得知点E在⊙O内．

解答 解：在Rt△ACO中，∠C=90°，AC=4，OC=3，
∴OA=$\sqrt{A{C}^{2}+O{C}^{2}}$=5．
又∵E是AO的中点，
∴OE=$\frac{1}{2}$OA=$\frac{5}{2}$．
∵OE=$\frac{5}{2}$＜3=OC，
∴点E在⊙O内．

点评 本题考查了点与圆的位置关系以及勾股定理，解题的关键是找出OE的长度．本题属于基础题，难度不大，解决该题型题目时，根据解直角三角形求出点到圆心的距离，将其与半径进行比较即可得出结论．