题目内容
7.(1)计算:2$\sqrt{\frac{1}{3}}$×$\sqrt{9}$-$\sqrt{12}$+$\root{3}{\frac{7}{8}-1}$.(2)解不等式组$\left\{\begin{array}{l}{x+3>0}\\{2(x-1)+3≥3x}\end{array}\right.$,并判断x=$\sqrt{3}$是否为该不等式组的解.
分析 (1)先根据二次根式的乘法,二次根式的性质,立方根的定义求出每一部分的值,再合并即可;
(2)先求出不等式的解集,再求出不等式组的解集,最后判断即可
解答 解:(1)原式=2$\sqrt{\frac{1}{3}×9}$-2$\sqrt{3}$+$\root{3}{-\frac{1}{8}}$
=2$\sqrt{3}$-2$\sqrt{3}$-$\frac{1}{2}$
=-$\frac{1}{2}$;
(2)$\left\{\begin{array}{l}{x+3>0①}\\{2(x-1)+3≥3x②}\end{array}\right.$
∵解不等式①得:x>-3,
解不等式②得:x≤1,
∴不等式组的解集为-3<x≤1,
∵$\sqrt{3}$>1,
∴x=$\sqrt{3}$不是该不等式组的解.
点评 本题考查了实数的混合运算,解一元一次不等式组的解集的应用,能熟记知识点是解此题的关键,主要培养了学生的计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.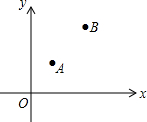 如图,在平面直角坐标系中,已知A(1,1)、B(3,5),要在y轴上找一点P,使得△PAB的周长最小,则点P的坐标为( )
如图,在平面直角坐标系中,已知A(1,1)、B(3,5),要在y轴上找一点P,使得△PAB的周长最小,则点P的坐标为( )
 如图,在平面直角坐标系中,已知A(1,1)、B(3,5),要在y轴上找一点P,使得△PAB的周长最小,则点P的坐标为( )
如图,在平面直角坐标系中,已知A(1,1)、B(3,5),要在y轴上找一点P,使得△PAB的周长最小,则点P的坐标为( )| A. | (0,1) | B. | (0,2) | C. | ($\frac{4}{3}$,0) | D. | (2,0) |
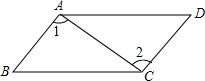 如图,在四边形ABCD中,∠BAD=∠BCD,∠1=∠2,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠BAD=∠BCD,∠1=∠2,求证:四边形ABCD是平行四边形. 如图,直线a,b被直线c所截,若a∥b,∠1=42°,则∠2=138度.
如图,直线a,b被直线c所截,若a∥b,∠1=42°,则∠2=138度.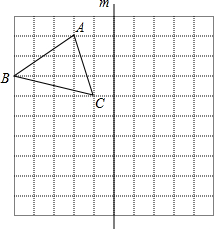 如图所示的正方形网格中,每个小正方形的边长均为1个单位,△ABC的三个顶点都在格点上.
如图所示的正方形网格中,每个小正方形的边长均为1个单位,△ABC的三个顶点都在格点上.