��Ŀ����
4�� ��ͼ����ABC����BCΪ�ױߵĵ��������Σ���A��C�ֱ���һ�κ���$y=-\frac{3}{4}x+3$��ͼ����y�ᡢx��Ľ��㣬��B�ڶ��κ���$y=\frac{1}{8}{x^2}+bx+c$��ͼ���ϣ��Ҹö��κ���ͼ���ϴ���һ��Dʹ�ı���ABCD�ܹ���ƽ���ı��Σ�
��ͼ����ABC����BCΪ�ױߵĵ��������Σ���A��C�ֱ���һ�κ���$y=-\frac{3}{4}x+3$��ͼ����y�ᡢx��Ľ��㣬��B�ڶ��κ���$y=\frac{1}{8}{x^2}+bx+c$��ͼ���ϣ��Ҹö��κ���ͼ���ϴ���һ��Dʹ�ı���ABCD�ܹ���ƽ���ı��Σ���1������b��c��ֵ����д���ö��κ����Ľ���ʽ��
��2������P��A��D��ͬʱ����Q��C��A����ÿ��1����λ���ٶ��˶����ʣ�
�ٵ�P�˶����δ�ʱ����APQ��ֱ�������Σ�
�ڵ�P�˶����δ�ʱ���ı���PDCQ�������С����ʱ�ı���PDCQ������Ƕ��٣�
���� ��1�����ȵó�B��D�����꣬�����ô���ϵ����������κ�������ʽ���ɣ�
��2���ٷֱ����õ�PQ��ACʱ����QP��ADʱ����Ϲ��ɶ������t��ֵ���ɣ�
�ڹ���Q��QH��AD������ΪH������S��APQ=$\frac{1}{2}$AP•QH=$\frac{1}{2}$AP•AQsin��PAQ��S��ACD=$\frac{1}{2}$AD•OA������S�ı���PDCQ=S��ACD-S��APQ�����ֵ���ɣ�
��� 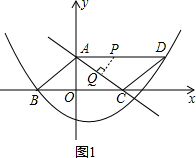 �⣺��1����$y=-\frac{3}{4}x+3$����A��0��3����C��4��0����
�⣺��1����$y=-\frac{3}{4}x+3$����A��0��3����C��4��0����
����B��C����OA�Գƣ�����B��-4��0����BC=8��
��ΪAD��BC��AD=BC������D��8��3����
��B��-4��0����D��8��3���ֱ����$y=\frac{1}{8}{x^2}+bx+c$��
��$\left\{\begin{array}{l}2-4b+c=0\\ 8+8b+c=3.\end{array}\right.$
��� $b=-\frac{1}{4}$��c=-3��
���Ըö��κ����Ľ���ʽΪ$y=\frac{1}{8}{x^2}-\frac{1}{4}x-3$��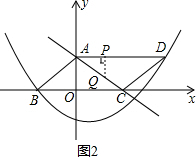
��2�������P��Q�˶���ʱ��Ϊt��
�ڡ�APQ�У�AP=t��AQ=AC-CQ=5-t��cos��PAQ=cos��ACO=$\frac{4}{5}$��
��PQ��ACʱ��$\frac{AQ}{AP}=\frac{4}{5}$��
����$\frac{5-t}{t}$=$\frac{4}{5}$��
���t=$\frac{25}{9}$����AP=$\frac{25}{9}$������ͼ1��ʾ��
��QP��ADʱ����ʱ$\frac{AP}{AQ}=\frac{4}{5}$��
����$\frac{t}{5-t}=\frac{4}{5}$��
���$t=\frac{20}{9}$����ͼ2��ʾ����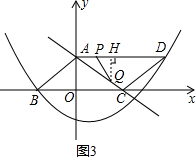
����ͼ3������Q��QH��AD������ΪH��
����S��APQ=$\frac{1}{2}AP•QH=\frac{1}{2}AP•AQsin��PAQ=\frac{1}{2}t��5-t����\frac{3}{5}=-\frac{3}{10}{t^2}+\frac{3}{2}t$
S��ACD=$\frac{1}{2}AD•OA=\frac{1}{2}��8��3=12$��
����S�ı���PDCQ=S��ACD-S��APQ=$12-��-\frac{3}{10}{t^2}+\frac{3}{2}t��=\frac{3}{10}{��t-\frac{5}{2}��^2}+\frac{81}{8}$��
���Ե�AP=$\frac{5}{2}$ʱ���ı���PDCQ�������Сֵ��$\frac{81}{8}$��
���� ������Ҫ�����˶��κ����ۺ��Լ�ֱ�������ε������Լ����κ�����ֵ��֪ʶ���������ν���Լ��������۵ó��ǽ���ؼ���

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| A�� | ��-1��2�� | B�� | ��1��2�� | C�� | ��-2��-1�� | D�� | ��2��-1�� |
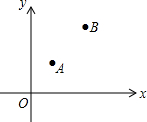 ��ͼ����ƽ��ֱ������ϵ�У���֪A��1��1����B��3��5����Ҫ��y������һ��P��ʹ�á�PAB���ܳ���С�����P������Ϊ��������
��ͼ����ƽ��ֱ������ϵ�У���֪A��1��1����B��3��5����Ҫ��y������һ��P��ʹ�á�PAB���ܳ���С�����P������Ϊ��������| A�� | ��0��1�� | B�� | ��0��2�� | C�� | ��$\frac{4}{3}$��0�� | D�� | ��2��0�� |
| A�� | 10 | B�� | 11 | C�� | 16 | D�� | 26 |
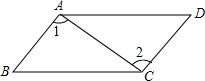 ��ͼ�����ı���ABCD�У���BAD=��BCD����1=��2����֤���ı���ABCD��ƽ���ı��Σ�
��ͼ�����ı���ABCD�У���BAD=��BCD����1=��2����֤���ı���ABCD��ƽ���ı��Σ� ��ͼ��ֱ��a��b��ֱ��c���أ���a��b����1=42�㣬���2=138�ȣ�
��ͼ��ֱ��a��b��ֱ��c���أ���a��b����1=42�㣬���2=138�ȣ�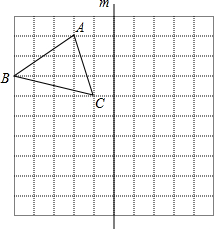 ��ͼ��ʾ�������������У�ÿ��С�����εı߳���Ϊ1����λ����ABC���������㶼�ڸ���ϣ�
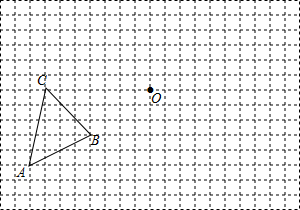
��ͼ��ʾ�������������У�ÿ��С�����εı߳���Ϊ1����λ����ABC���������㶼�ڸ���ϣ�