题目内容
17.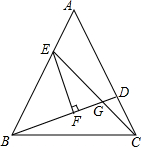 如图,等边△ABC中,AE=CD,EF⊥BD,若FG=$\sqrt{3}$,则EF等于( )
如图,等边△ABC中,AE=CD,EF⊥BD,若FG=$\sqrt{3}$,则EF等于( )| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 3 | D. | 4 |
分析 只要证明△AEC≌△CDB(SAS),推出∠EGB=60°即可解决问题.
解答 证明:∵△ABC为等边三角形,
∴AC=BC,∠A=∠ACB=60°,
在△AEC和△CDB中,
$\left\{\begin{array}{l}{AE=CD}\\{∠A=∠ACB}\\{AC=CB}\end{array}\right.$,
∴△AEC≌△CDB(SAS),
∴∠ACE=∠CBD,
∵∠ACE+∠ECB=60°,
∴∠CBD+∠ECB=60°,
∵∠EGB为△GBC的外角,
∴∠EGB=60°,
∴在Rt△EFP中,∠GEF=30°,
则EF=$\sqrt{3}$FG=3,
故选C.
点评 本题考查等边三角形的性质、全等三角形的判定与性质、直角三角形30度角性质等知识,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
7.反比例函数y=$\frac{k}{x}$,若k<0,则( )
| A. | y的值为负 | |
| B. | 双曲线在一、三象限 | |
| C. | y随x的增大而增大 | |
| D. | 在所在的每一个象限,y随x的增大而增大 |
8. 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )
 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )| A. | 圆锥 | B. | 四棱锥 | C. | 圆柱 | D. | 四棱柱 |
5.在平面直角坐标系中,已知菱形ABCD的三个顶点的坐标为A(m,0),B(0,5),C(-m,0),则点D的坐标为( )
| A. | (0,m) | B. | (0,-m) | C. | (0,-5) | D. | (m,5) |
12. 如图,把直尺沿直线断开并错位,点E、D、B、F在同一直线上,若∠ADE=135°,则∠DBC的度数是( )
如图,把直尺沿直线断开并错位,点E、D、B、F在同一直线上,若∠ADE=135°,则∠DBC的度数是( )
 如图,把直尺沿直线断开并错位,点E、D、B、F在同一直线上,若∠ADE=135°,则∠DBC的度数是( )
如图,把直尺沿直线断开并错位,点E、D、B、F在同一直线上,若∠ADE=135°,则∠DBC的度数是( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
2.若a>b,则下列式子正确的是( )
| A. | -2a>-2b | B. | $\frac{a}{2}$<$\frac{b}{2}$ | C. | 4-a<4-b | D. | a-4<b-4 |
9.若x2+a-x是关于x的完全平方式,则a的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 1 | D. | -$\frac{1}{4}$ |
6.下列计算正确的是( )
| A. | x+x2=x3 | B. | x6÷x3=x2 | C. | 2x+3x=5x | D. | (x3)2=x5 |
7.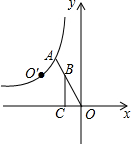 如图,点A是双曲线y=-$\frac{2}{x}$(x<0)上的一点,连结OA,在线段OA上取一点B,作BC⊥x轴于点C,以BC的中点为对称中心,作点O的中心对称点O′,当O′落在这条双曲线上时,$\frac{OA}{OB}$的值为( )
如图,点A是双曲线y=-$\frac{2}{x}$(x<0)上的一点,连结OA,在线段OA上取一点B,作BC⊥x轴于点C,以BC的中点为对称中心,作点O的中心对称点O′,当O′落在这条双曲线上时,$\frac{OA}{OB}$的值为( )
 如图,点A是双曲线y=-$\frac{2}{x}$(x<0)上的一点,连结OA,在线段OA上取一点B,作BC⊥x轴于点C,以BC的中点为对称中心,作点O的中心对称点O′,当O′落在这条双曲线上时,$\frac{OA}{OB}$的值为( )
如图,点A是双曲线y=-$\frac{2}{x}$(x<0)上的一点,连结OA,在线段OA上取一点B,作BC⊥x轴于点C,以BC的中点为对称中心,作点O的中心对称点O′,当O′落在这条双曲线上时,$\frac{OA}{OB}$的值为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |