题目内容
5.在平面直角坐标系中,已知菱形ABCD的三个顶点的坐标为A(m,0),B(0,5),C(-m,0),则点D的坐标为( )| A. | (0,m) | B. | (0,-m) | C. | (0,-5) | D. | (m,5) |
分析 构建中点坐标公式,设D(x,y),由四边形ABCD是平行四边形,可知AC与BD互相平分,则有$\left\{\begin{array}{l}{\frac{0+x}{2}=\frac{m+(-m)}{2}}\\{\frac{5+y}{2}=\frac{0+0}{2}}\end{array}\right.$,解方程组即可解决问题.
解答 解:设D(x,y),
∵四边形ABCD是平行四边形,
∴AC与BD互相平分,
则有$\left\{\begin{array}{l}{\frac{0+x}{2}=\frac{m+(-m)}{2}}\\{\frac{5+y}{2}=\frac{0+0}{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=0}\\{y=-5}\end{array}\right.$,
∴点D坐标为(0,-5).
故选C.
点评 本题考查菱形的性质、坐标与图象的性质、中点坐标公式,方程组等知识,解题的关键是灵活运用菱形的性质,构建方程组解决问题,属于中考常考题型.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
15.下列调查,适合用普查方式的是( )
| A. | 调查全市初中学生的每天课外阅读时间 | |
| B. | 调查全市学生每天的睡眠时间 | |
| C. | 调查全市初中学生的视力情况 | |
| D. | 调查一个班级学生的身高 |
16.已知两圆的半径分别为1和5,圆心距为4,那么两圆的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
13. 如图,点A.B.C在⊙D上,∠ABC=70°,则∠ADC的度数为( )
如图,点A.B.C在⊙D上,∠ABC=70°,则∠ADC的度数为( )
 如图,点A.B.C在⊙D上,∠ABC=70°,则∠ADC的度数为( )
如图,点A.B.C在⊙D上,∠ABC=70°,则∠ADC的度数为( )| A. | 110° | B. | 140° | C. | 35° | D. | 130° |
20.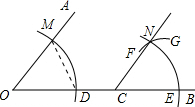 如图,点C落在射线OB上,用尺规作CN∥OA,需要以点E为圆心,作弧FG,其半径的长应截取( )
如图,点C落在射线OB上,用尺规作CN∥OA,需要以点E为圆心,作弧FG,其半径的长应截取( )
 如图,点C落在射线OB上,用尺规作CN∥OA,需要以点E为圆心,作弧FG,其半径的长应截取( )
如图,点C落在射线OB上,用尺规作CN∥OA,需要以点E为圆心,作弧FG,其半径的长应截取( )| A. | 线段OD的长 | B. | 线段OM的长 | C. | 线段DM的长 | D. | 线段CE的长 |
10.下列各多项式中,能用公式法因式分解的是( )
| A. | -b2+2ab | B. | 25n2+10n | C. | 9-6a+a2 | D. | a2+b2+2a |
17.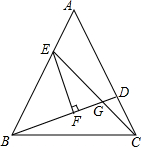 如图,等边△ABC中,AE=CD,EF⊥BD,若FG=$\sqrt{3}$,则EF等于( )
如图,等边△ABC中,AE=CD,EF⊥BD,若FG=$\sqrt{3}$,则EF等于( )
 如图,等边△ABC中,AE=CD,EF⊥BD,若FG=$\sqrt{3}$,则EF等于( )
如图,等边△ABC中,AE=CD,EF⊥BD,若FG=$\sqrt{3}$,则EF等于( )| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 3 | D. | 4 |
14.甲、乙两人练习跑步,若乙先跑10米,则甲跑5秒就能追上乙,若乙先跑2秒,则甲跑4秒就可追上乙.设甲,乙每秒分别跑x米,y米,则下列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{5(x-y)=10}\\{4(x-y)=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{5x-5y=-10}\\{4x-4y=2}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{5x-5y=10}\\{4x-4y=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{5x-5y=10}\\{4x=6y}\end{array}\right.$ |
15.为了求1+2+22+23+…+22016的值,可令S=1+2+22+23+…+22016,则2S=2+22+23+24+…+22017,因此2S-S=22017-1,所以1+2+22+23+…+22016=22017-1.仿照以上推理计算出1+5+52+53+…+52016的值是( )
| A. | 52016-1 | B. | 52017-1 | C. | $\frac{{{5^{2016}}-1}}{4}$ | D. | $\frac{{{5^{2017}}-1}}{4}$ |