题目内容
10. 如图,在直角坐标系中,已知点A的坐标为(6,0),点B(x,y)在第一象限内,且满足x+y=8,设△AOB的面积是S.
如图,在直角坐标系中,已知点A的坐标为(6,0),点B(x,y)在第一象限内,且满足x+y=8,设△AOB的面积是S.(1)写出S与x的函数关系式,并写出x的取值范围;
(2)当S=18时,求出点B的坐标;
(3)点B在何处时,△AOB是等腰三角形?
分析 (1)由点B在第一象限且满足x+y=8,即可得出y=-x+8(0<x<8),再根据三角形的面积公式即可得出S关于x的函数关系式;
(2)将S=18代入(1)的结论中,求出x值,即可得出点B的坐标;
(3)由点O、A、B的坐标利用两点间的距离公式求出OA、OB、AB的长度,分OA=OB、OA=AB和OB=AB三种情况考虑△AOB为等腰三角形,由线段相等可得出关于x的无理方程,解方程即可得出x值,将其代入点B的坐标即可得出结论.
解答 解:(1)∵点B(x,y)在第一象限内,且满足x+y=8,
∴y=-x+8(0<x<8).
S=$\frac{1}{2}$OA•y=$\frac{1}{2}$×6•(-x+8)=-3x+24(0<x<8).
(2)令S=-3x+24中S=18,则-3x+24=18,
解得:x=2,y=-x+8=6,
∴点B的坐标为(2,6).
(3)∵O(0,0),A(6,0),B(x,-x+8),
∴OA=6,OB=$\sqrt{{x}^{2}+(-x+8)^{2}}$,AB=$\sqrt{(x-6)^{2}+(-x+8)^{2}}$.
△AOB为等腰三角形分三种情况:
①当OA=OB时,有6=$\sqrt{{x}^{2}+(-x+8)^{2}}$,
解得:${x}_{1}=4+\sqrt{2}$,x2=4-$\sqrt{2}$,
此时点B的坐标为(4+$\sqrt{2}$,4-$\sqrt{2}$)或(4-$\sqrt{2}$,4+$\sqrt{2}$);
②当OA=AB时,有6=$\sqrt{(x-6)^{2}+(-x+8)^{2}}$,
解得:x3=7-$\sqrt{17}$,x4=7+$\sqrt{17}$(舍去),
此时点B的坐标为(7-$\sqrt{17}$,$\sqrt{17}$-1);
③当OB=AB时,有$\sqrt{{x}^{2}+(-x+8)^{2}}$=$\sqrt{(x-6)^{2}+(-x+8)^{2}}$,
解得:x5=3,
此时点B的坐标为(3,5).
综上可知:点B的坐标为(4+$\sqrt{2}$,4-$\sqrt{2}$)、(4-$\sqrt{2}$,4+$\sqrt{2}$)、(7-$\sqrt{17}$,$\sqrt{17}$-1)或(3,5)时,△AOB是等腰三角形.
点评 本题考查了一次函数图象上点的坐标特征、三角形的面积公式以及解无理方程,解题的关键是:(1)用x表示出y,并得出x的取值范围;(2)代入S=18求出x值;(3)分OA=OB、OA=AB和OB=AB三种情况考虑.本题属于中档题,难度不大,解决该题型题目时,根据等腰三角形的性质,分三条边两两相等来考虑.

 如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )
如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
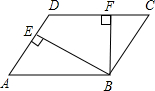 如图,在菱形ABCD中,BE⊥AD于E,BF⊥CD于F,且AE=DE,则∠EBF的度数是( )
如图,在菱形ABCD中,BE⊥AD于E,BF⊥CD于F,且AE=DE,则∠EBF的度数是( )| A. | 75° | B. | 60° | C. | 50° | D. | 45° |
 如图,AB是⊙O的直径,AC是弦,OP⊥AC于点D,交⊙O于点E,连接BE、CE,∠P=∠BEC.
如图,AB是⊙O的直径,AC是弦,OP⊥AC于点D,交⊙O于点E,连接BE、CE,∠P=∠BEC. 已知:如图,AB∥CD,∠A=∠D.求证:AF∥ED.
已知:如图,AB∥CD,∠A=∠D.求证:AF∥ED. 如图,在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E.
如图,在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E.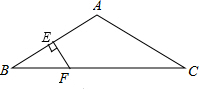 如图,△ABC中,AB=AC,∠A=120°,AB的垂直平分线EF交AB于E,交BC于F.求证:CF=2BF.
如图,△ABC中,AB=AC,∠A=120°,AB的垂直平分线EF交AB于E,交BC于F.求证:CF=2BF.