题目内容
 如图,在平行四边形ABCD中,BD=CD,∠A=75°,CE⊥BD于E,求∠BCE的度数.
如图,在平行四边形ABCD中,BD=CD,∠A=75°,CE⊥BD于E,求∠BCE的度数.考点:平行四边形的性质
专题:
分析:在△BCD中可求出∠CBD=∠BCD=75°,在Rt△BCE中即可求出∠BCE的度数.
解答:解:∵四边形ABCD是平行四边形,∠A=75°(已知)
∴∠BCD=∠A=75°(平行四边形的对角相等)
∵BD=CD(已知)
∴∠DBC=∠BCD=75°(等边对等角)
∵CE⊥BD(已知)
∴∠CEB=90°
∴∠BCE=90°-75°=15°.
∴∠BCD=∠A=75°(平行四边形的对角相等)
∵BD=CD(已知)
∴∠DBC=∠BCD=75°(等边对等角)
∵CE⊥BD(已知)
∴∠CEB=90°
∴∠BCE=90°-75°=15°.
点评:此题考查了平行四边形的性质、三角形的内角和定义、等腰三角形的性质,综合考查的知识点较多,解答本题的关键是得出∠DBC的度数,难度一般.

练习册系列答案
相关题目
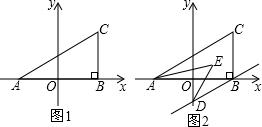 如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+
如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)2+
 如图所示为三个同心圆组成的图形,AB⊥CD,AB与CD交于原点O,且点A、B的坐标分别为(-2,0)、(2,0).求阴影部分的面积.
如图所示为三个同心圆组成的图形,AB⊥CD,AB与CD交于原点O,且点A、B的坐标分别为(-2,0)、(2,0).求阴影部分的面积.