题目内容
1.阅读:(x-1)(x+1)=x2-1,(x-1)(x2+x+1)=x3-1,(x-1)(x3+x2+x+1)=x4-1.由上面的规律得(x-1)(xn+xn-1+…+x+1)=xn+1-1(n为正整数);
根据这一规律进行计算:22014-22013+22012-22011+22010…-23+22-2+1=$\frac{{2}^{2015}+1}{3}$.
分析 (1)根据阅读知识找到规律即可求解;
(2)原式变形为-$\frac{1}{3}$(-2-1)×[(-2)2014+(-2)2013+(-2)2012+(-2)2011+(-2)2010…+(-2)3+(-2)2+(-2)+1],计算即可得到结果.
解答 解:(1)(x-1)×(xn+xn-1+…+x+1)=xn+1-1(n为正整数);
(2)22014-22013+22012-22011+22010…-23+22-2+1
=-$\frac{1}{3}$×(-2-1)×[(-2)2014+(-2)2013+(-2)2012+(-2)2011+(-2)2010…+(-2)3+(-2)2+(-2)+1]
=-$\frac{1}{3}$×[(-2)2015-1]
=$\frac{{2}^{2015}+1}{3}$.
故答案为:xn+1-1;$\frac{{2}^{2015}+1}{3}$.
点评 此题考查了平方差公式,弄清题中的规律是解本题的关键.

练习册系列答案
相关题目
6.一个食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表,现有15升食物需要存放且要求每个盒子要装满.由于A型号盒子正要做促销活动,购买三个及三个以上可一次性返现金4元,则购买盒子所需要最少费用为29元.
| 型号 | A | B |
| 单个盒子容量(升) | 2 | 3 |
| 单价(元) | 5 | 6 |
11.一次函数y=kx+3的自变量取值增加2,函数值就相应减少2,则k的值为( )
| A. | 2 | B. | -2 | C. | -1 | D. | 4 |
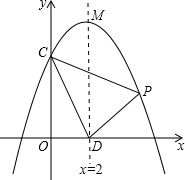 如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD,
如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD,