题目内容
6.一个食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表,现有15升食物需要存放且要求每个盒子要装满.由于A型号盒子正要做促销活动,购买三个及三个以上可一次性返现金4元,则购买盒子所需要最少费用为29元.| 型号 | A | B |
| 单个盒子容量(升) | 2 | 3 |
| 单价(元) | 5 | 6 |
分析 设购买A种型号盒子x个,购买盒子所需要费用为y元,则购买B种盒子的个数为$\frac{15-2x}{3}$个,分0≤x<3和3≤x两种情况考虑,分别找出y关于x的函数关系式,再利用一次函数的性质即可解答.
解答 解:设购买A种型号盒子x个,购买盒子所需要费用为y元,则购买B种盒子的个数为$\frac{15-2x}{3}$个,
①当0≤x<3时,y=5x+$\frac{15-2x}{3}$×6=x+30,
∵k=1>0,
∴y随x的增大而增大,
∴当x=0时,y有最小值,最小值为30元;
②当3≤x时,y=5x+$\frac{15-2x}{3}$×6-4=26+x,
∵k=1>0,
∴y随x的增大而增大,
∴当x=3时,y有最小值,最小值为29元;
综合①②可得,购买盒子所需要最少费用为29元.
故答案为:29.
点评 本题考查了列代数式以及一次函数的性质,分别0≤x<3和3≤x两种情况找出y关于x的函数关系式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知点P(m+1,m-4)在x轴上,那么点P的坐标是( )
| A. | (4,0) | B. | (0,-5) | C. | (0,5) | D. | (5,0) |
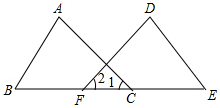 在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.
在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.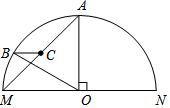 如图MN为半圆O的直径,半径OA⊥MN,C为AM的中点,过C点作BC∥MN交⊙O于点B.
如图MN为半圆O的直径,半径OA⊥MN,C为AM的中点,过C点作BC∥MN交⊙O于点B.