题目内容
13．先观察：1-$\frac{1}{{2}^{2}}$=$\frac{1}{2}$×$\frac{3}{2}$，1-$\frac{1}{{3}^{2}}$=$\frac{2}{3}$×$\frac{4}{3}$，1-$\frac{1}{{4}^{2}}$=$\frac{3}{4}$×$\frac{5}{4}$，…（1）探究规律填空：1-$\frac{1}{{n}^{2}}$=$\frac{n-1}{n}$×$\frac{n+1}{n}$；
（2）计算：（1-$\frac{1}{{2}^{2}}$）•（1-$\frac{1}{{3}^{2}}$）•（1-$\frac{1}{{4}^{2}}$）…（1-$\frac{1}{201{5}^{2}}$）
分析 （1）利用平方差公式变形即可得到结果；
（2）原式利用平方差公式化简，计算即可得到结果．
解答 解：（1）原式=$\frac{n-1}{n}$×$\frac{n+1}{n}$；
（2）原式=（1-$\frac{1}{2}$）（1+$\frac{1}{2}$）（1-$\frac{1}{3}$）（1+$\frac{1}{3}$）…（1-$\frac{1}{2015}$）（1+$\frac{1}{2015}$）
=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×…×$\frac{2014}{2015}$×$\frac{2016}{2015}$
=$\frac{1008}{2015}$，
故答案为：（1）$\frac{n-1}{n}$；$\frac{n+1}{n}$
点评 此题考查了有理数的混合运算，熟练掌握平方差公式是解本题的关键．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
已知等边△ABC中，点D，E分别在边AB，BC上，把△BDE沿直线DE翻折，使点B落在点B′处，DB′，EB′分别交边AC于点F，G，若∠ADF=60°，则∠EGC的度数为60°．
3．某学校组织了一次“五城联创”知识竞赛活动，根据初赛成绩分别从三个年级中选出了10名同学参加决赛，成绩统计如下：
（1）补全下面的表格：
（2）从以下两个方面对三个年纪的成绩进行评价：
①从平均数和众数方面分析，八年级成绩较好；
②从中位数和众数方面分析，七年级成绩较好；
（3）学校决定根据决赛成绩，从某个年级中选出3人参加总决赛，你认为该选取哪个年纪的学生参赛？并写出理由．
| 决赛成绩（单位：分） | |
| 七年级 | 82 86 88 81 88 97 80 74 90 89 |
| 八年级 | 85 88 87 97 85 76 88 80 86 88 |
| 九年级 | 81 83 79 79 79 92 99 88 89 86 |
| 年纪 | 平均数 | 众数 | 中位数 |
| 七年级 | 85.5 | 88 | 87 |
| 八年级 | 86 | 88 | 86.5 |
| 九年级 | 85.5 | 79 | 84.5 |
①从平均数和众数方面分析，八年级成绩较好；
②从中位数和众数方面分析，七年级成绩较好；
（3）学校决定根据决赛成绩，从某个年级中选出3人参加总决赛，你认为该选取哪个年纪的学生参赛？并写出理由．
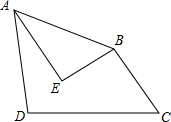如图，在四边形ABCD中，AB=AD，∠BAD=∠C=60°，点E为四边形ABCD内部一点，连接AE、BE，∠AEB=∠CBE=90°，BC=3，则线段BE的长为$\frac{3\sqrt{3}}{2}$．