题目内容
11.抛物线y=$\frac{1}{2}$x2-x+m与x轴交于A,B两点,与y轴交于点C,其顶点在直线y=-2x上.(1)求m的值;
(2)求△ABC的面积.
分析 (1)首先根据公式求得对称轴,即顶点的横坐标,代入y=-2x即可求得顶点坐标,然后代入抛物线的解析式求得m的值;
(2)求得A、B以及C的坐标,然后利用三角新的面积公式求解.
解答 解:(1)抛物线的对称轴是x=1,
把x=1代入y=-2x得y=-2,
则顶点坐标是(1,-2),
把(1,-2)代入函数解析式得$\frac{1}{2}$-1+m=-2,
解得:m=-$\frac{3}{2}$;
(2)函数的解析式是y=$\frac{1}{2}$x2-x-$\frac{3}{2}$,
令y=0,得$\frac{1}{2}$x2-x-$\frac{3}{2}$=0,
解得:x1=-1,x2=3;
则AB=3-(-1)=4,
在y=$\frac{1}{2}$x2-x-$\frac{3}{2}$中令x=0,解得y=-$\frac{3}{2}$,
则S△ABC=$\frac{1}{2}$×4×$\frac{3}{2}$=3.
点评 本题考查了二次函数与x轴的交点的求法,求与x轴的交点坐标时,令y=0,解方程即可求得与x轴的交点的横坐标.

练习册系列答案
相关题目
 如图,在Rt△ABC中,AC=5,BC=12,将Rt△ABC沿AD折叠后,使点C落在AB上的点E处,求CD.
如图,在Rt△ABC中,AC=5,BC=12,将Rt△ABC沿AD折叠后,使点C落在AB上的点E处,求CD.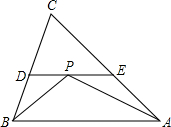 如图,△ABC中,∠ABC,∠CAB的平分线交于点P,过点P作DE∥AB,分别交BC,AC于点D,E.
如图,△ABC中,∠ABC,∠CAB的平分线交于点P,过点P作DE∥AB,分别交BC,AC于点D,E.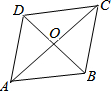 如图,?ABCD 的对角线AC,BD相交于点,且AC=4,BD=$2\sqrt{3}$,AB=$\sqrt{7}$.试证明四边形ABCD是菱形.
如图,?ABCD 的对角线AC,BD相交于点,且AC=4,BD=$2\sqrt{3}$,AB=$\sqrt{7}$.试证明四边形ABCD是菱形.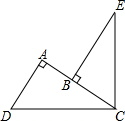 如图,∠DCE=90°,∠DAC=90°,BE⊥AC于点B,且DC=EC,请证明:AB+AD=BE.
如图,∠DCE=90°,∠DAC=90°,BE⊥AC于点B,且DC=EC,请证明:AB+AD=BE. 如图,△ABD、△AEC都是等边三角形,BE=4cm,求DC.
如图,△ABD、△AEC都是等边三角形,BE=4cm,求DC.