题目内容
19．
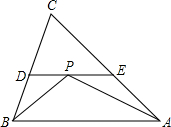如图，△ABC中，∠ABC，∠CAB的平分线交于点P，过点P作DE∥AB，分别交BC，AC于点D，E．求证：DE=BD+AE．
分析 由平行线的性质结合角平分线的定义可证明DB=DP，PE=AE，可证得结论．
解答 证明：∵BP平分∠CBA，
∴∠DBP=∠ABP，
∵DE∥AB，
∴∠DPB=∠ABP，
∴∠DBP=∠DPB，
∴BD=PD，
同理可得PE=EA，
∴DE=DP+PE=BD+AE．
点评 本题主要考查等腰三角形的判定和性质，由平行线的性质和角平分线的定义证得BD=DP、PE=AE是解题的关键．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
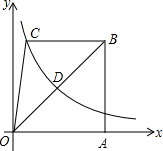如图，已知梯形ABCO的底边AO在x轴上，BC∥AO，AB⊥AO，过点C的双曲线y=$\frac{k}{x}$交OB于D，且OD：DB=1：2．若△OBC的面积等于8，则k的值为2．
如图，Rt△AOB的一条直角边OB在x轴上，双曲线y=$\frac{k}{x}$（x＞0）经过斜边OA的中点C，与另一直角边交于点D，若S△OCD=6，则S△OBD的值为4．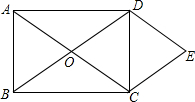
如图，长方形ABCD中，线段AC、BD相交于点O，DE∥AC，CE∥BD，BC=2cm，那么三角形EDC可以看作由△OAB平移得到的，连接OE，则OE=2cm．
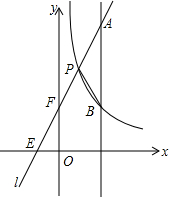如图，一次函数y1=kx+b的图象l与坐标轴分别交于点E、F，与函数y2=$\frac{4}{x}$（x＞0）的图象交于点P（1，m），且F是PE的中点