题目内容
16.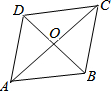 如图,?ABCD 的对角线AC,BD相交于点,且AC=4,BD=$2\sqrt{3}$,AB=$\sqrt{7}$.试证明四边形ABCD是菱形.
如图,?ABCD 的对角线AC,BD相交于点,且AC=4,BD=$2\sqrt{3}$,AB=$\sqrt{7}$.试证明四边形ABCD是菱形.
分析 由平行四边形的对角线互相平分得到△AOB的两条边OA、OB的长度,则根据勾股定理的逆定理判定∠AOB=90°,即平行四边形的对角线互相垂直平分,故四边形ABCD是菱形.
解答 证明:∵四边形ABCD是平行四边形,AC=4,BD=2$\sqrt{3}$,
∴OA=$\frac{1}{2}$AC=2,OB=$\frac{1}{2}$BD=$\sqrt{3}$.
又∵AB=$\sqrt{7}$,
∴AB2=OA2+OB2=7,
∴∠AOB=90°,即AC⊥BD,
∴平行四边形ABCD的对角线互相垂直平分,
∴平行四边形ABCD是菱形.
点评 本题考查了菱形的判定.对角线互相垂直的平行四边形是菱形(或“对角线互相垂直平分的四边形是菱形”)以及勾股定理的逆定理运用,解题的关键是能够证明AC⊥BD.

练习册系列答案
相关题目
 如图,求图中∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I度数的和为540°.
如图,求图中∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I度数的和为540°.
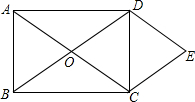 如图,长方形ABCD中,线段AC、BD相交于点O,DE∥AC,CE∥BD,BC=2cm,那么三角形EDC可以看作由△OAB平移得到的,连接OE,则OE=2cm.
如图,长方形ABCD中,线段AC、BD相交于点O,DE∥AC,CE∥BD,BC=2cm,那么三角形EDC可以看作由△OAB平移得到的,连接OE,则OE=2cm. 如图,CD=AB,AE=CF,DE=BF,求证:AB∥CD.
如图,CD=AB,AE=CF,DE=BF,求证:AB∥CD.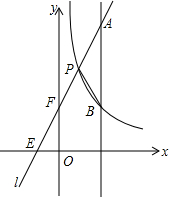 如图,一次函数y1=kx+b的图象l与坐标轴分别交于点E、F,与函数y2=$\frac{4}{x}$(x>0)的图象交于点P(1,m),且F是PE的中点
如图,一次函数y1=kx+b的图象l与坐标轴分别交于点E、F,与函数y2=$\frac{4}{x}$(x>0)的图象交于点P(1,m),且F是PE的中点 如图,在?ABCD中,EF∥BC,MN∥CD,EF与MN相交于点O,除外,图中还有8个平行四边形.
如图,在?ABCD中,EF∥BC,MN∥CD,EF与MN相交于点O,除外,图中还有8个平行四边形. 图中△ABE和△ACD都是等边三角形.问AE与BD的大小关系是?如果要△ABE和△ACD全等,则还需要什么条件?
图中△ABE和△ACD都是等边三角形.问AE与BD的大小关系是?如果要△ABE和△ACD全等,则还需要什么条件?