题目内容
3.(1)某校计划修建一条400米长的跑道,实际开工后每天比原计划多修10米,结果比原计划提前2天完成了任务,求原计划每天修多少米?(2)小明准备了4张形状、大小完全相同的不透明卡片,上面分别写有整数-50、40、30、-20,将这4张卡片写有整数的一面向下放在桌面上.从中任意抽取两张,抽到的数是(1)中的分式方程的解的概率.
分析 (1)原计划每天修x米,利用时间列等量关系得到$\frac{400}{x+10}$=$\frac{400}{x}$-2,然后解方程、检验,最后确定问题的答案;
(2)先画树状图展示所有12种等可能的结果数,再找出抽到的数为40和-50的结果数,然后根据概率公式求解.
解答 解:(1)设原计划每天修x米,
根据题意得$\frac{400}{x+10}$=$\frac{400}{x}$-2,
解得x1=40,x2=-50,
经检验x1=40,x2=-50都是原方程的解,
而x=-50<0,不合题意舍去,
所以x=40,
答:原计划每天修40米;
(2)画树状图为:
共有12种等可能的结果数,其中抽到的数为40和-50的结果数为2种,
所以从中任意抽取两张,抽到的数是(1)中的分式方程的解的概率=$\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.也考查了分式方程的应用.

练习册系列答案
相关题目
12.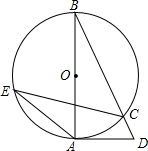 如图,AB为⊙O的直径,点E、C都在圆上,连接AE,CE,BC,过点A作⊙O的切线交BC的延长线于点D,若∠AEC=25°,则∠D的度数为( )
如图,AB为⊙O的直径,点E、C都在圆上,连接AE,CE,BC,过点A作⊙O的切线交BC的延长线于点D,若∠AEC=25°,则∠D的度数为( )
 如图,AB为⊙O的直径,点E、C都在圆上,连接AE,CE,BC,过点A作⊙O的切线交BC的延长线于点D,若∠AEC=25°,则∠D的度数为( )
如图,AB为⊙O的直径,点E、C都在圆上,连接AE,CE,BC,过点A作⊙O的切线交BC的延长线于点D,若∠AEC=25°,则∠D的度数为( )| A. | 75° | B. | 65° | C. | 55° | D. | 74° |
13.浙江省正在进行五水共治工程,今年乐清市政府决定投资2630万元用于河流改造,还给市民清山绿水.将2630万元用科学记数法表示为( )元.
| A. | 26.3×106 | B. | 2.63×107 | C. | 2.63×106 | D. | 26.3×107 |
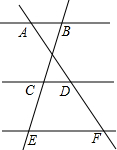 如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长是$\frac{24}{5}$.
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长是$\frac{24}{5}$.