题目内容
15. 如图,在 Rt△ABC中,∠ABC是直角,AB=4,BC=2$\sqrt{5}$,P是BC边上的动点,设BP=x,若能在AC边上找到一点Q,使∠BQP=90°,则x的取值范围是$\frac{8\sqrt{5}}{5}$≤x≤2$\sqrt{5}$.
如图,在 Rt△ABC中,∠ABC是直角,AB=4,BC=2$\sqrt{5}$,P是BC边上的动点,设BP=x,若能在AC边上找到一点Q,使∠BQP=90°,则x的取值范围是$\frac{8\sqrt{5}}{5}$≤x≤2$\sqrt{5}$.
分析 先根据勾股定理计算出AC=6,由于∠BQP=90°,根据圆周角定理得到点Q在以PB为直径的圆⊙M上,而点Q在AC上,则有AC与⊙M相切于点Q,连结MQ,根据切线的性质得MQ⊥AC,MQ=BM=$\frac{1}{2}$x,然后证明Rt△CMQ∽Rt△CAB,再利用相似比得到$\frac{1}{2}$x:4=(2$\sqrt{5}$-$\frac{1}{2}$x):6,最后解方程即可.
解答 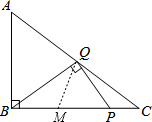 解:∵∠ABC=90°,AB=4,BC=2$\sqrt{5}$,
解:∵∠ABC=90°,AB=4,BC=2$\sqrt{5}$,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=6,
∵∠BQP=90°,
∴点Q在以PB为直径的圆⊙M上,
∵点Q在AC上,
∴AC与⊙M相切于点Q,
连结MQ,如图,则MQ⊥AC,MQ=BM=$\frac{1}{2}$x,
∵∠QCM=∠BCA,
∴Rt△CMQ∽Rt△CAB,
∴QM:AB=CM:AC,即$\frac{1}{2}$x:4=(2$\sqrt{5}$-$\frac{1}{2}$x):6,
∴x=$\frac{8\sqrt{5}}{5}$.
当P与C重合时,BP=2$\sqrt{5}$,
∴BP=x的取值范围是:$\frac{8\sqrt{5}}{5}$≤x≤2$\sqrt{5}$,
故答案为:$\frac{8\sqrt{5}}{5}$≤x≤2$\sqrt{5}$.
点评 本题考查了直线与圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,则直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.也考查了勾股定理和相似三角形的判定与性质.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
7.二次函数y=-x2+2x+c的图象与x轴有两个交点A(x1,0),B(x2,0),且x1<x2,点P(m,n)是图象上一点,那么下列判断正确的是( )
| A. | 当n<0时,m<x1 | B. | 当n<0时,m>x2 | C. | 当n>0时,x1<m<x2 | D. | 当n>0时,m>x1 |
5.用120厘米长的铁丝围成一个直角三角形,这个三角形三条边长度的比是3:4:5,这个直角三角形的面积是( )平方厘米.
| A. | 1000 | B. | 1200 | C. | 600 | D. | 2000 |
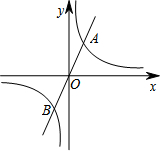 如图,直线y=kx(k>0)与双曲线y=$\frac{3}{x}$交于A、B两点,若A、B两点的坐标分别为A(x1,y1),B(x2,y2),则x1y2+x2y1的值为-6.
如图,直线y=kx(k>0)与双曲线y=$\frac{3}{x}$交于A、B两点,若A、B两点的坐标分别为A(x1,y1),B(x2,y2),则x1y2+x2y1的值为-6.
 如图,△ABC中,AB=4,∠BAC=30°,若在AC、AB上各取一点M、N使BM+MN的值最小,则这个最小值为2$\sqrt{3}$.
如图,△ABC中,AB=4,∠BAC=30°,若在AC、AB上各取一点M、N使BM+MN的值最小,则这个最小值为2$\sqrt{3}$.