题目内容
5.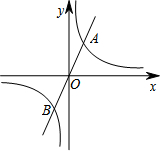 如图,直线y=kx(k>0)与双曲线y=$\frac{3}{x}$交于A、B两点,若A、B两点的坐标分别为A(x1,y1),B(x2,y2),则x1y2+x2y1的值为-6.
如图,直线y=kx(k>0)与双曲线y=$\frac{3}{x}$交于A、B两点,若A、B两点的坐标分别为A(x1,y1),B(x2,y2),则x1y2+x2y1的值为-6.
分析 先根据点A(x1,y1),B(x2,y2)是双曲线y=$\frac{3}{x}$上的点可得出x1•y1=x2•y2=3,再根据直线y=kx(k>0)与双曲线y=$\frac{3}{x}$交于点A(x1,y1),B(x2,y2)两点可得出x1=-x2,y1=-y2,再把此关系代入所求代数式进行计算即可.
解答 解:∵点A(x1,y1),B(x2,y2)是双曲线y=$\frac{3}{x}$上的点,
∴x1•y1=x2•y2=3①,
∵直线y=kx(k>0)与双曲线y=$\frac{3}{x}$交于点A(x1,y1),B(x2,y2)两点,
∴x1=-x2,y1=-y2②,
∴原式=-x1y1-x2y2=-3-3=-6.
故答案为:-6.
点评 本题考查的是反比例函数与一次函数的交点问题,反比例函数的对称性,根据反比例函数的图象关于原点对称得出x1=-x2,y1=-y2是解答此题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
7. 如图,以正方形ABCD的对角线AC为边作菱形AEFC,点E在边AB的延长线上,则∠FAE的度数等于( )
如图,以正方形ABCD的对角线AC为边作菱形AEFC,点E在边AB的延长线上,则∠FAE的度数等于( )
 如图,以正方形ABCD的对角线AC为边作菱形AEFC,点E在边AB的延长线上,则∠FAE的度数等于( )
如图,以正方形ABCD的对角线AC为边作菱形AEFC,点E在边AB的延长线上,则∠FAE的度数等于( )| A. | 15° | B. | 22.5° | C. | 30° | D. | 37.5° |
16.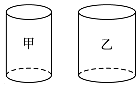 如图,在水平桌面上有甲、乙两个内部呈圆柱形的容器,内部底面积分别为80cm 2、100cm 2,且甲容器装满水,乙容器是空的.若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲的水位高度低了8cm,则甲的容积是( )
如图,在水平桌面上有甲、乙两个内部呈圆柱形的容器,内部底面积分别为80cm 2、100cm 2,且甲容器装满水,乙容器是空的.若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲的水位高度低了8cm,则甲的容积是( )
 如图,在水平桌面上有甲、乙两个内部呈圆柱形的容器,内部底面积分别为80cm 2、100cm 2,且甲容器装满水,乙容器是空的.若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲的水位高度低了8cm,则甲的容积是( )
如图,在水平桌面上有甲、乙两个内部呈圆柱形的容器,内部底面积分别为80cm 2、100cm 2,且甲容器装满水,乙容器是空的.若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲的水位高度低了8cm,则甲的容积是( )| A. | 1280 cm 3 | B. | 2560 cm 3 | C. | 3200 cm 3 | D. | 4000 cm 3 |
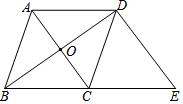 如图,在菱形ABCD中,对角线AC、BD相交于点O,且AB=5,AC=6,过点D作AC的平行线交BC的延长线于点E,则△BDE的面积为24.
如图,在菱形ABCD中,对角线AC、BD相交于点O,且AB=5,AC=6,过点D作AC的平行线交BC的延长线于点E,则△BDE的面积为24.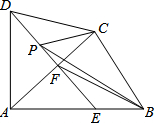 如图四边形ABCD中,AD=DC,∠DAB=∠ACB=90°,过点D作DF⊥AC,垂足为F.DF与AB相交于E.设AB=15,BC=9,P是射线DF上的动点.当△BCP的周长最小时,DP的长为12.5.
如图四边形ABCD中,AD=DC,∠DAB=∠ACB=90°,过点D作DF⊥AC,垂足为F.DF与AB相交于E.设AB=15,BC=9,P是射线DF上的动点.当△BCP的周长最小时,DP的长为12.5. 如图,在△ABC中,AC边的垂直平分线交BC于点D,若AC=4cm,△ABC的周长为13cm,则△ABD的周长为9cm.
如图,在△ABC中,AC边的垂直平分线交BC于点D,若AC=4cm,△ABC的周长为13cm,则△ABD的周长为9cm. 如图,在 Rt△ABC中,∠ABC是直角,AB=4,BC=2$\sqrt{5}$,P是BC边上的动点,设BP=x,若能在AC边上找到一点Q,使∠BQP=90°,则x的取值范围是$\frac{8\sqrt{5}}{5}$≤x≤2$\sqrt{5}$.
如图,在 Rt△ABC中,∠ABC是直角,AB=4,BC=2$\sqrt{5}$,P是BC边上的动点,设BP=x,若能在AC边上找到一点Q,使∠BQP=90°,则x的取值范围是$\frac{8\sqrt{5}}{5}$≤x≤2$\sqrt{5}$.