题目内容
11.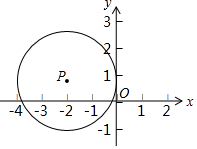 如图,在直角坐标系中,点P的坐标为(-2,1),⊙P与y轴相切,求⊙P在x轴上截得的弦长.
如图,在直角坐标系中,点P的坐标为(-2,1),⊙P与y轴相切,求⊙P在x轴上截得的弦长.
分析 首先如图:过点P作PA⊥x轴于点A,连接PB,PC,由点P的坐标为(-2,1),⊙P与y轴相切,利用勾股定理即可求得AC的长,然后由垂径定理求得答案.
解答  解:如图:过点P作PA⊥x轴于点A,连接PB,PC,
解:如图:过点P作PA⊥x轴于点A,连接PB,PC,
∵点P的坐标为(-2,1),⊙P与y轴相切,
∴PA=1,PB=PC=2,
∴AC=$\sqrt{P{C}^{2}-P{A}^{2}}$=$\sqrt{3}$,
∴⊙P在x轴上截得的弦长为:2$\sqrt{3}$.
点评 此题考查了切线的性质以及垂径定理.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
3. ①若点A、B、C在数轴上分别表示-1、4、c,且点C到点A、B的距离之和是7,则c=5或-2;
①若点A、B、C在数轴上分别表示-1、4、c,且点C到点A、B的距离之和是7,则c=5或-2;
②关于x的方程|x-m|+|x-n|=k(m>n,k>0),借助数轴探究方程的解的情况,直接写出结论.
 ①若点A、B、C在数轴上分别表示-1、4、c,且点C到点A、B的距离之和是7,则c=5或-2;
①若点A、B、C在数轴上分别表示-1、4、c,且点C到点A、B的距离之和是7,则c=5或-2;②关于x的方程|x-m|+|x-n|=k(m>n,k>0),借助数轴探究方程的解的情况,直接写出结论.
16.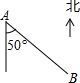 如图,货轮A与灯塔B相距40 nmile,下列灯塔B相对于货轮A的位置的描述中,准确的是( )
如图,货轮A与灯塔B相距40 nmile,下列灯塔B相对于货轮A的位置的描述中,准确的是( )
 如图,货轮A与灯塔B相距40 nmile,下列灯塔B相对于货轮A的位置的描述中,准确的是( )
如图,货轮A与灯塔B相距40 nmile,下列灯塔B相对于货轮A的位置的描述中,准确的是( )| A. | 南偏东50° | B. | 南偏东50°且距货轮40 nmile处 | ||
| C. | 距灯塔40 nmile处 | D. | 北偏西50°且距货轮40 nmile处 |
