题目内容
12．
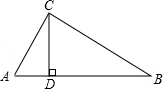如图，在△ABC中，∠ACB=90°，CD⊥AB，垂足为D，若∠B=30°，CD=6，求AB的长．
分析 根据直角三角形的性质得到BC=2CD=12，根据余弦的定义计算即可．
解答 解：∵CD⊥AB，∠B=30°，
∴BC=2CD=12，
∴AB=$\frac{BC}{cos30°}$=8$\sqrt{3}$．
点评 本题考查的是直角三角形的性质，掌握直角三角形中，30°角所对的直角边等于斜边的一半是解题的关键．
练习册系列答案
优等生题库系列答案
相关题目
2．如果甲数为x，乙数比甲数多4倍，则乙数为（ ）
| A． | 4x | B． | 5x | C． | $\frac{1}{4}$x | D． | $\frac{1}{5}$x |
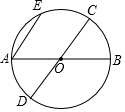已知：如图，AB，CD是⊙O的直径，AE是⊙O的弦，若AE∥CD，求证：$\widehat{AD}$=$\widehat{BC}$=$\widehat{EC}$．
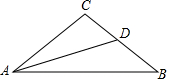已知：如图，在△ABC中，AC=BC，∠C=100°，AD平分∠CAB．