题目内容
10.已知直线l1经过点(2,3)和点(-2,1),直线l2经过点(-1,4)和点(2,1),直线l1,l2,l3交于同一点,且直线l3经过点(4,0).求直线l3对应的函数表达式.分析 设直线l1解析式为:y1=k1x+b1 将点(2,3)和点(-2,1)代入联立方程组解得解析式;同理可得l2 解析式,再由直线l1,l2,l3交于同一点,联立l1 和l2解析式可得交点坐标,再将所求交点坐标和点(4,0),利用待定系数法解得表达式.
解答 解:设直线l1解析式为:y1=k1x+b1 将点(2,3)和点(-2,1)代入可得
$\left\{\begin{array}{l}{3={2k}_{1}{+b}_{1}}\\{1=-{2k}_{1}{+b}_{1}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{1}=\frac{1}{2}}\\{{b}_{1}=2}\end{array}\right.$,
∴直线l1 解析式为:y=$\frac{1}{2}x+2$;
同理可得直线l2 解析式为:y=-x+3
∵直线l1,l2,l3交于同一点,
∴$\left\{\begin{array}{l}{y=\frac{1}{2}x+2}\\{y=-x+3}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=\frac{2}{3}}\\{y=\frac{7}{3}}\end{array}\right.$,
∴直线l3经过点($\frac{2}{3}$,$\frac{7}{3}$)和点(4,0),
设直线l3的解析式为:y=kx+b,将点($\frac{2}{3}$,$\frac{7}{3}$)和点(4,0)代入得,
$\left\{\begin{array}{l}{\frac{7}{3}=\frac{2}{3}k+b}\\{0=4k+b}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=-\frac{7}{10}}\\{b=\frac{14}{5}}\end{array}\right.$,
∴直线l3对应的函数表达式为:y=$-\frac{7}{10}x+\frac{14}{5}$.
点评 本题主要考查了待定系数法求一次函数的解析式,关键是联立方程组求得交点.

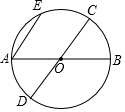 已知:如图,AB,CD是⊙O的直径,AE是⊙O的弦,若AE∥CD,求证:$\widehat{AD}$=$\widehat{BC}$=$\widehat{EC}$.
已知:如图,AB,CD是⊙O的直径,AE是⊙O的弦,若AE∥CD,求证:$\widehat{AD}$=$\widehat{BC}$=$\widehat{EC}$.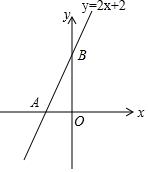 如图所示,直线y=2x+2与x轴交于点A,与y轴交于点B.
如图所示,直线y=2x+2与x轴交于点A,与y轴交于点B.