题目内容
17.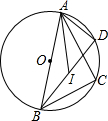 如图,△ABC内接于⊙O,AB为⊙O的直径,点I是△ABC的内心,延长BI交⊙O于D,若AC=4,BC=3,求BI•ID的值.
如图,△ABC内接于⊙O,AB为⊙O的直径,点I是△ABC的内心,延长BI交⊙O于D,若AC=4,BC=3,求BI•ID的值.
分析 过点D作DE⊥AB于E,过点D作DF⊥BC于F,连接DC,先利用全等三角形证明BE=BF,AE=CF,求出BE、AE、AD,再证明△ADI是等腰直角三角形,最后求出BI、DI即可解决问题.
解答 解:过点D作DE⊥AB于E,过点D作DF⊥BC于F,连接DC,
∵点I是△ABC的内心,
∴∠BAI=∠CAI,∠ABI=∠CBI,
∵∠DAC=∠DBC,∴∠ABI=∠DAC,
∴∠DAI=∠DAC+∠IAC=∠ABI+∠BAI=∠AID,
∴AD=DI;
∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°.
∵AC=4,BC=3,
∴AB=5.
在△BED和△BFD中,
$\left\{\begin{array}{l}{∠EBD=∠FBD}\\{∠BED=∠BFD}\\{BD=BD}\end{array}\right.$,
∴△BED≌△BFD(AAS),
∴DE=DF,BE=BF.
∵∠ABD=∠CBD,
∴DA=DC,
∴AE2=AD2-DE2=DC2-DF2=CF2,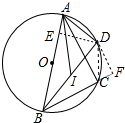
∴AE=CF,
∴AB-BE=BF-BC,
∴5-BE=BE-3,
∴BE=4,
∴AE=AB-BE=5-4=1.
∵∠DAE=∠BAD,∠AED=∠ADB=90°,
∴△AED∽△ADB,
∴$\frac{AD}{AB}$=$\frac{AE}{AD}$,
∴AD2=AE•AB=1×5=5,
∵AD>0
∴AD=DI=$\sqrt{5}$,
在RT△ABD中,∵∠ADB=90°,AD=$\sqrt{5}$,AB=5,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{{5}^{2}-(\sqrt{5})^{2}}$=2$\sqrt{5}$,
∴BI=BD-DI=2$\sqrt{5}$-$\sqrt{5}$=$\sqrt{5}$,
∴BI•DI=$\sqrt{5}$•$\sqrt{5}$=5.
点评 本题主要考查内心、全等三角形的判定和性质、勾股定理、圆周角定理、相似三角形的判定与性质、勾股定理等知识,综合性比较强,解题的关键是添加辅助线构造全等三角形,求出线段AE、BE、AD,属于中考压轴题.

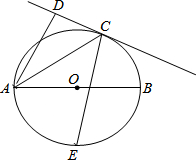 如图,AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD,垂足为D,E是弧AB的中点,若AD=$\frac{32}{5}$,AC=8,则CE的长为( )
如图,AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD,垂足为D,E是弧AB的中点,若AD=$\frac{32}{5}$,AC=8,则CE的长为( )| A. | 7$\sqrt{2}$ | B. | 7$\sqrt{3}$ | C. | 8$\sqrt{2}$ | D. | 3+4$\sqrt{2}$ |
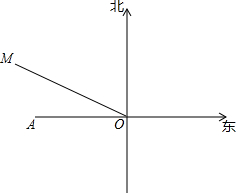 如图,根据天气预报,台风中心位于A市正东方向300km的点O处,正以20km/h的速度向北偏西60°方向移动,距离台风中心250km范围内都会受到影响,若台风移动的速度和方向不变,则A市受台风影响的时间是有多长?
如图,根据天气预报,台风中心位于A市正东方向300km的点O处,正以20km/h的速度向北偏西60°方向移动,距离台风中心250km范围内都会受到影响,若台风移动的速度和方向不变,则A市受台风影响的时间是有多长?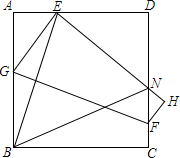 如图,四边形ABCD是正方形,E是AD边上一点,将正方形折叠,使点B与点E重合,FG是折痕,C点落在H上,EH与CD交于点N.求证:∠EBN=45°.
如图,四边形ABCD是正方形,E是AD边上一点,将正方形折叠,使点B与点E重合,FG是折痕,C点落在H上,EH与CD交于点N.求证:∠EBN=45°.
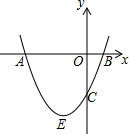 如图,抛物线y=x2+bx+c与y轴交于点C,与x轴交于点A,B,点A在点B的左侧,点A的坐标为A(-3,0),且AB=4.
如图,抛物线y=x2+bx+c与y轴交于点C,与x轴交于点A,B,点A在点B的左侧,点A的坐标为A(-3,0),且AB=4.