题目内容
2.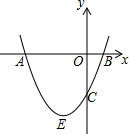 如图,抛物线y=x2+bx+c与y轴交于点C,与x轴交于点A,B,点A在点B的左侧,点A的坐标为A(-3,0),且AB=4.
如图,抛物线y=x2+bx+c与y轴交于点C,与x轴交于点A,B,点A在点B的左侧,点A的坐标为A(-3,0),且AB=4.(1)求抛物线的解析式;
(2)若过点C且与x轴平行的直线交抛物线于另一个点D,抛物线的顶点为点E,试判断△CDE的形状,并求其面积.
分析 (1)先利用A点坐标和AB=4得到B点坐标,然后利用交点式可写出抛物线解析式;
(2)如图,通过计算自变量为0时的函数值可得C点坐标,把(1)中抛物线解析式配成顶点式得到抛物线的对称轴和顶点E的坐标,再利用对称性得到D点坐标,然后运用勾股定理的逆定理证明△CDE为等腰直角三角形,最后根据三角形面积公式计算S△CDE.
解答 解:(1)∵点A的坐标为(-3,0),且AB=4,
∴B(1,0),
∴抛物线解析式为y=(x+3)(x-1),即y=x2+2x-3;
(2)如图,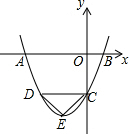
当x=0时,y=x2+2x-3=-3,则C(0,-3),
∵y=x2+2x-3=(x+1)2-4,
∴抛物线的对称轴为直线x=-1,顶点E的坐标为(-1,-4),
∵DE∥x轴,
∴点C与点D关于直线x=-1对称,
∴D(-2,-3),
∵CD2=4,CE2=12+(-3+4)2=2,DE2=(-2+1)2+(-3+4)2=2,
∴CD2=CE2+DE2,CE=DE,
∴△CDE为等腰直角三角形,
S△CDE=$\frac{1}{2}$•2•1=2.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.解决(2)小题的关键是运用勾股定理的逆定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
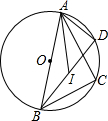 如图,△ABC内接于⊙O,AB为⊙O的直径,点I是△ABC的内心,延长BI交⊙O于D,若AC=4,BC=3,求BI•ID的值.
如图,△ABC内接于⊙O,AB为⊙O的直径,点I是△ABC的内心,延长BI交⊙O于D,若AC=4,BC=3,求BI•ID的值.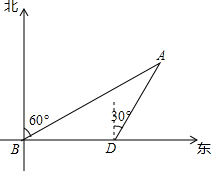 如图,海中有一小岛A,它的周围10海里内有暗礁,渔船由西向东航行.在B点测得小岛A在北偏东60°方向,再航行12海里到达D点,这时测得小岛A在北偏东30°方向.如果渔船不改变航向,继续向东航行,有没有触礁的危险?
如图,海中有一小岛A,它的周围10海里内有暗礁,渔船由西向东航行.在B点测得小岛A在北偏东60°方向,再航行12海里到达D点,这时测得小岛A在北偏东30°方向.如果渔船不改变航向,继续向东航行,有没有触礁的危险?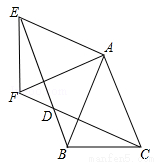
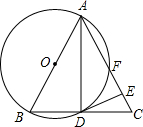 如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与AC交于点F,过点D作⊙O的切线交AC于E.
如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与AC交于点F,过点D作⊙O的切线交AC于E.