题目内容
3.解不等式(组)(1)解不等式 10-3(x+6)≤1;
(2)解不等式组$\left\{\begin{array}{l}2x+5≤3(x+2)(1)\\ \frac{x-1}{2}<\frac{x}{3}(2)\end{array}\right.$,并将解集表示在数轴上.
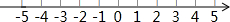
分析 (1)去括号,移项,合并同类项,系数化成1即可;
(2)先求出每个不等式的解集,再找出不等式组的解集即可.
解答 解:(1)10-3(x+6)≤1,
10-3x-18≤1,
-3x≤1-10+18,
-3x≤9,
x≥-3;
(2)$\left\{\begin{array}{l}2x+5≤3(x+2)(1)\\ \frac{x-1}{2}<\frac{x}{3}(2)\end{array}\right.$,
∵解不等式(1)得:x≥-1,
解不等式(2)得:x<3,
∴不等式组的解集为-1≤x<3,
把不等式组的解集在数轴上表示为: .
.
点评 本题考查了解一元一次不等式和解一元一次不等式组、在数轴上表示不等式组的解集的应用,能正确运用不等式的性质解一元一次不等式和能根据不等式的解集找出不等式组的解集是解此题的关键,难度适中.

练习册系列答案
相关题目
8. 如图,AB∥CD,DB⊥BC,∠1=30°,则∠2的度数是( )
如图,AB∥CD,DB⊥BC,∠1=30°,则∠2的度数是( )
 如图,AB∥CD,DB⊥BC,∠1=30°,则∠2的度数是( )
如图,AB∥CD,DB⊥BC,∠1=30°,则∠2的度数是( )| A. | 40° | B. | 50° | C. | 60° | D. | 140° |
13.若2x-1=16,则x等于( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
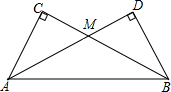 把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点,这时MC的长度就等于点M到AB的距离.你知道这是为什么吗?
把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点,这时MC的长度就等于点M到AB的距离.你知道这是为什么吗?
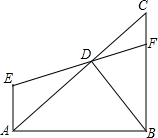 如图,∠ABC=90°,AE∥BC,D为AC上的一点,连接ED并延长交BC于点F,且∠ABD=∠DAE,问:BD与AC的位置关系如何?说明理由.
如图,∠ABC=90°,AE∥BC,D为AC上的一点,连接ED并延长交BC于点F,且∠ABD=∠DAE,问:BD与AC的位置关系如何?说明理由.