题目内容
11．
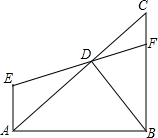如图，∠ABC=90°，AE∥BC，D为AC上的一点，连接ED并延长交BC于点F，且∠ABD=∠DAE，问：BD与AC的位置关系如何？说明理由．
分析 BD与AC垂直，理由为：由AE与BC平行得到一对内错角相等，由已知角相等等量代换得到∠ABD=∠C，再由一对公共角相等，得到三角形ABD与三角形ACB相似，利用相似三角形对应角相等得到∠ADB为直角，即可得证．
解答 解：BD⊥AC，理由为：
证明：∵AE∥BC，
∴∠DAE=∠C，
∵∠ABD=∠DAE，
∴∠DAE=∠C，
∵∠BAD=∠CAB，
∴△ABD∽△ACB，
∴∠ADB=∠ABC=90°，
∴BD⊥AC．
点评 此题考查了平行线的性质，以及垂线，熟练掌握平行线的性质是解本题的关键．
练习册系列答案
相关题目
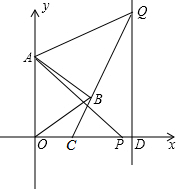如图，已知等边△AOB的顶点O与原点重合，点A的坐标为（0，2$\sqrt{3}$），点P（t，0）为x轴上一动点（不与O重合）．连结AP，将AP绕点A逆时针旋转60°得到线段AQ，连结QB并延长交x轴于点C．过Q作x轴的垂线，垂足为D．
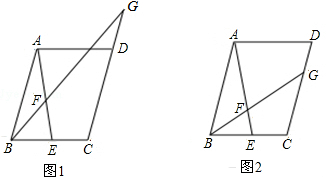
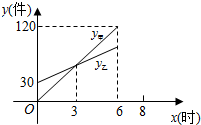甲、乙两人合作加工一批零件．乙先加工30件后，甲开始加工．设甲的加工量为y甲（件），乙的加工量为y乙（件），甲的加工时间记为x（时），y甲、y乙分别与x之间的部分函数图象如图所示．