题目内容
15.设a=-|-2|,b=-(-2),c=$\root{3}{-27}$,则a,b,c中最小的实数是c.分析 首先求出a、b、c的大小,然后根据正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小,据此判断即可.
解答 解:a=-|-2|=-2,b=-(-2)=2,c=$\root{3}{-27}$=-3,
∵-3<-2<2,
∴c<a<b,
∴a,b,c中最小的实数是c.
故答案为:c.
点评 (1)此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.
(2)此题还考查了一个数的绝对值的求法,以及一个数的三次方根的计算,要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列各点中在过点(-3,2)和(-3,4)的直线上的是( )
| A. | (-3,0) | B. | (0,-3) | C. | (3,2) | D. | (5,4) |
4.下列语句不是命题的是( )
| A. | 垂线段最短 | B. | 同位角相等 | ||
| C. | 过点P作线段AB的垂线 | D. | 不相等的角一定不是对顶角 |
5. 如图,已知a∥b,∠1=65°,则∠2的度数为( )
如图,已知a∥b,∠1=65°,则∠2的度数为( )
 如图,已知a∥b,∠1=65°,则∠2的度数为( )
如图,已知a∥b,∠1=65°,则∠2的度数为( )| A. | 115° | B. | 125° | C. | 65° | D. | 25° |
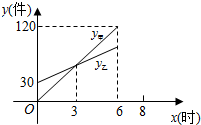 甲、乙两人合作加工一批零件.乙先加工30件后,甲开始加工.设甲的加工量为y甲(件),乙的加工量为y乙(件),甲的加工时间记为x(时),y甲、y乙分别与x之间的部分函数图象如图所示.
甲、乙两人合作加工一批零件.乙先加工30件后,甲开始加工.设甲的加工量为y甲(件),乙的加工量为y乙(件),甲的加工时间记为x(时),y甲、y乙分别与x之间的部分函数图象如图所示.