题目内容
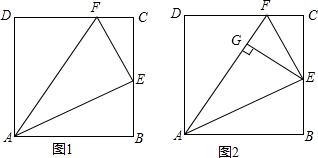
15.在正方形ABCD中,AB=4,E为BC的中点,F在CD上,DF=3CF,连结AF、AE、EF.(1)如图1,求出△AEF的三条边的长度;
(2)判断△AEF的形状;并说明理由;
(3)探究S△ECF+S△ABE与S△AEF的关系,并说明理由;
(4)如图2,作EG⊥AF于G,
①试求出FG、AG、EG的长度;
②试探究EG2与FG×AG的关系?并说明理由.
分析 (1)先求得EC、FC、DF、BE、AD的长,然后依据勾股定理可求得EF、EB、AE的长;
(2)由勾股定理的逆定理可证明△EFA为直角三角形;
(3)依据三角形的面积公式分别求得△AEF、△ECF、△ABE的面积,从而可得出问题的答案;
(4)①依据三角形的面积公式可知S△AEF=$\frac{1}{2}$AF•GE=5,从而可求得EG的长,然后再依据勾股定理可求得FG的长,然后可得到AG的长;②求得EG2、GF•AG的结果,从而可得到它们之间的关系.
解答 解:(1)∵ABCD为正方形,AB=4,
∴AB=BC=DC=AD=4.
∵E是BC的中点,
∴BE=CE=2.
∵CD=4,DF=3CF,
∴FC=1,DF=3.
依据勾股定理可知:EF=$\sqrt{F{C}^{2}+C{E}^{2}}$=$\sqrt{5}$,AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=2$\sqrt{5}$,AF=$\sqrt{A{D}^{2}+D{F}^{2}}$=5.
(2)∵AF2=25,EF2=5,AE2=20,
∴AF2=EF2+AE2.
∴△AEF为直角三角形.
(3)S△AEF=S△ECF+S△ABE.
理由:∵S△ECF=$\frac{1}{2}$FC•CE=$\frac{1}{2}$×1×2=1,S△ABE=$\frac{1}{2}$AB•BE=$\frac{1}{2}$×4×2=4,S△AEF=$\frac{1}{2}$EF•AE=$\frac{1}{2}$×$\sqrt{5}$×2$\sqrt{5}$=5,
∴S△AEF=S△ECF+S△ABE.
(4)①∵S△AEF=$\frac{1}{2}$AF•GE=5,
∴$\frac{1}{2}$×5×EG=5.
∴EG=2.
在△EFG中,由勾股定理可知:FG=$\sqrt{E{F}^{2}-G{E}^{2}}$=$\sqrt{(\sqrt{5})^{2}-{2}^{2}}$=1.
AG=AF-GF=5-1=4.
②∵EG2=22=4,GF•AG=1×4=4,
∴EG2=GF•AG.
点评 本题主要考查的是正方形的性质、勾股定理的应用、勾股定理的逆定理的应用、三角形的面积公式的应用,依据勾股定理的逆定理判断出△AEF为直角三角形是解题的关键.

| A. | x3-x2=x | B. | x3•x2=x6 | C. | x3÷x2=x | D. | (x3)2=x5 |
| 人 数 | 1 | 3 | 5 | 70 | 10 | 8 | 3 |
| 金额(元) | 200000 | 150000 | 80000 | 15000 | 10000 | 8000 | 5000 |
| A. | 极差是195000 | B. | 中位数是15000 | C. | 众数是15000 | D. | 平均数是15000 |
| A. | 互相重合 | B. | 互相平行 | C. | 互相垂直 | D. | 无法确定 |
| A. | 2-2=$\frac{1}{4}$ | B. | 2-2=-$\frac{1}{4}$ | C. | (-2-2)3=-$\frac{1}{6}$ | D. | -(2-2)3=$\frac{3}{4}$ |
| A. | 能够完全重合 | B. | 三边对应相等 | ||
| C. | 两角及一边对应相等 | D. | 两边及一角对应相等 |
