题目内容
3.已知 xy=6,x+y=-4,求x$\sqrt{\frac{x}{y}}$+y$\sqrt{\frac{y}{x}}$的值.分析 先利用有理数的性质得到x<0,y<0,再根据二次根式的性质化简得到原式═-$\frac{x\sqrt{xy}}{y}$-$\frac{y\sqrt{xy}}{x}$,然后利用完全平方公式变形得到原式=-$\sqrt{xy}$•$\frac{(x+y)^{2}-2xy}{xy}$,再利用整体代入的方法计算.
解答 解:∵xy=6>0,
∴x,y 同号.
又 x+y=-4<0,
∴x<0,y<0,
∴原式=x$\sqrt{\frac{xy}{{y}^{2}}}$+y$\sqrt{\frac{xy}{{x}^{2}}}$
=-$\frac{x\sqrt{xy}}{y}$-$\frac{y\sqrt{xy}}{x}$
=-$\sqrt{xy}$•$\frac{(x+y)^{2}-2xy}{xy}$
=-$\sqrt{6}$•$\frac{(-4)^{2}-2×6}{6}$
=-$\frac{2\sqrt{6}}{3}$.
点评 本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
7.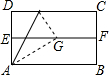 如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
 如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )
如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平;再一次折叠,使点D落到EF上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
8.地球与月球的平均距离为384 000km,将384 000这个数用科学记数法表示为( )
| A. | 3.84×103 | B. | 3.84×104 | C. | 3.84×105 | D. | 3.84×106 |
8.已知4<a<7,$\sqrt{(a-4)^{2}}+\sqrt{(a-7)^{2}}$化简后为( )
| A. | 3 | B. | -3 | C. | 2a-11 | D. | 11-2a |
12.若M-(-N)=0,则M与N的关系是( )
| A. | 互为相反数 | B. | 大小相等 | C. | M>N | D. | M<N |
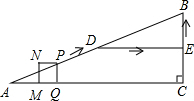 如图,在Rt△ABC中,∠ACB=90°,AC=16cm,BC=12cm.D、E分别为边AB、BC的中点,连接DE.点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在线段AD上以5cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M在线段AQ上.设点P的运动时间为t(s).
如图,在Rt△ABC中,∠ACB=90°,AC=16cm,BC=12cm.D、E分别为边AB、BC的中点,连接DE.点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在线段AD上以5cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M在线段AQ上.设点P的运动时间为t(s).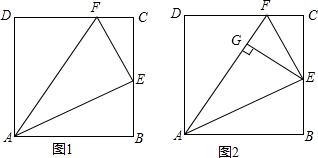
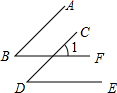 如图所示,AB∥CD,∠B=∠D,求证:BF∥DE(请在括号或横线上填空)
如图所示,AB∥CD,∠B=∠D,求证:BF∥DE(请在括号或横线上填空)