题目内容
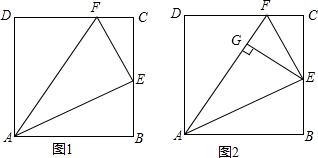
6.已知在△ABC中,∠ABC=45°,AD⊥BC,且BD=4,高AD上有一动点E(点E不与点A、点D重合),联结BE并延长与边AC相交于点F.(1)当点E为AD中点,且BF⊥AC时,求AF;
(2)当DC=3,设DE=x,AF=y,请建立y与x的函数关系式,并写出定义域;
(3)在(2)的条件下,当△AEF为等腰三角形时,求DE的长.

分析 (1)利用勾股定理求出BE,再证明△BED∽△AEF,得到$\frac{AF}{BD}$=$\frac{AE}{BE}$,列出方程即可解决.
(2)作CK⊥BC,交BF的延长线于K,由AD∥KC,得到$\frac{ED}{CK}$=$\frac{BD}{BC}$,求出CK,代入$\frac{AE}{CK}$=$\frac{AF}{FC}$即可解决问题.
(3)只有AE=AF,列出方程即可解决.
解答 解:(1)∵AD⊥BD,∠ABD=45°,
∴BD=AD=4,
∵AE=ED=2,在RT△BED中,BE=$\sqrt{B{D}^{2}+D{E}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$.
∵∠BED=∠AEF,∠BDE=∠AFE=90°,
∴△BED∽△AEF,
∴$\frac{AF}{BD}$=$\frac{AE}{BE}$,
∴$\frac{AF}{4}$=$\frac{2}{2\sqrt{5}}$,
∴AF=$\frac{4\sqrt{5}}{5}$.
(2)作CK⊥BC,交BF的延长线于K.
∵AD⊥BC,
∴AD∥KC,
∴$\frac{ED}{CK}$=$\frac{BD}{BC}$,
∴$\frac{x}{CK}$=$\frac{4}{7}$,
∴CK=$\frac{7}{4}$x,
∵$\frac{AE}{CK}$=$\frac{AF}{FC}$,
∴$\frac{4-x}{\frac{7}{4}x}$=$\frac{y}{5-y}$,
∴y=$\frac{80-20x}{3x+16}$.(0<x<4).
(3)∵∠AEF>∠DAC,∠EFA>∠EAF,
∴只有可能∠AEF=∠AFE,
∴AE=AF,
∴4-x=$\frac{80-20x}{3x+16}$,
解得:x=$\frac{4}{3}$或4(舍弃).
∴当△AEF为等腰三角形时,DE的长为$\frac{4}{3}$.
点评 本题考查相似三角形综合题、平行线分线段成比例定理、勾股定理等知识,解题的关键是添加辅助线,利用平行线分线段成比例定理解决问题,属于中考常考题型.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | -1 | B. | 0 | C. | 2 | D. | 3 |
| A. | 3.84×103 | B. | 3.84×104 | C. | 3.84×105 | D. | 3.84×106 |
| A. | -1 | B. | 0 | C. | 1 | D. | -3 |

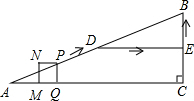 如图,在Rt△ABC中,∠ACB=90°,AC=16cm,BC=12cm.D、E分别为边AB、BC的中点,连接DE.点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在线段AD上以5cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M在线段AQ上.设点P的运动时间为t(s).
如图,在Rt△ABC中,∠ACB=90°,AC=16cm,BC=12cm.D、E分别为边AB、BC的中点,连接DE.点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在线段AD上以5cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M在线段AQ上.设点P的运动时间为t(s).