题目内容
10.解方程:(1)$\frac{x}{x-5}$=$\frac{x-2}{x-6}$
(2)$\frac{x+1}{x-1}$-$\frac{4}{{x}^{2}-1}$=1.
分析 (1)方程两边同乘以(x-5)(x-6)化为整式方程进行解答解可;
(2)方程两边同乘以(x+1)(x-1)化为整式方程进行解答解可.
解答 解:(1)$\frac{x}{x-5}$=$\frac{x-2}{x-6}$
方程两边同乘以(x-5)(x-6),得
x(x-6)=(x-2)(x-5)
解得,x=10.
检验:x=10时,(x-5)(x-6)≠0,
故原分式方程的解是x=10.
(2)$\frac{x+1}{x-1}$-$\frac{4}{{x}^{2}-1}$=1
方程两边同乘以(x+1)(x-1),得
(x+1)(x+1)-4=(x+1)(x-1)
解得,x=1
检验:x=1时,(x+1)(x-1)=0,
故原分式方程无解.
点评 本题考查解分式方程,解题的关键是将分式方程化为整式方程,注意要进行检验.

练习册系列答案
相关题目
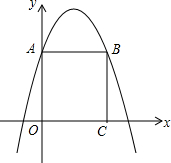 如图,在平面直角坐标系中,正方形ABCD的边长为2,抛物线y=ax2+bx+c经过A,B两点,且与x轴的一个交点坐标是(-$\frac{2}{9}$,0),求这个抛物线的解析式.
如图,在平面直角坐标系中,正方形ABCD的边长为2,抛物线y=ax2+bx+c经过A,B两点,且与x轴的一个交点坐标是(-$\frac{2}{9}$,0),求这个抛物线的解析式. 如图,点C、O、D在同一直线上,∠AOB=90°,∠BOD=25°,求∠AOC的度数.
如图,点C、O、D在同一直线上,∠AOB=90°,∠BOD=25°,求∠AOC的度数.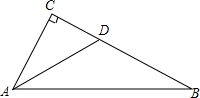 如图,在Rt△ABC中,∠C=90°,AD平分∠A,交边BC于点D,BD=2CD,求证:BC=$\sqrt{3}$•AC.
如图,在Rt△ABC中,∠C=90°,AD平分∠A,交边BC于点D,BD=2CD,求证:BC=$\sqrt{3}$•AC.