题目内容
5．
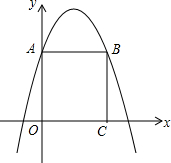如图，在平面直角坐标系中，正方形ABCD的边长为2，抛物线y=ax2+bx+c经过A，B两点，且与x轴的一个交点坐标是（-$\frac{2}{9}$，0），求这个抛物线的解析式．
分析 根据条件可得到A、B的坐标，然后运用待定系数法，就可求出抛物线的解析式．
解答 解：由题可得A（0，2），B（2，2）．
把（0，2）、（2，2）、（-$\frac{2}{9}$，0）代入y=ax2+bx+c，可得
$\left\{\begin{array}{l}{c=2}\\{4a+2b+c=2}\\{\frac{4}{81}a-\frac{2}{9}b+c=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=-\frac{81}{20}}\\{b=\frac{81}{10}}\\{c=2}\end{array}\right.$，
∴抛物线的解析式为y=-$\frac{81}{20}$x2+$\frac{81}{10}$x+2．
点评 本题主要考查的是运用待定系数法求二次函数的解析式、解三元一次方程组等知识，运用待定系数法是求函数解析式常用的方法，应熟练掌握．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
小学期末标准试卷系列答案
相关题目
15．食品厂从生产的袋张食品中抽样20袋，检测每袋的质量是否符合标准，超过或不足的部分分别用正，负数表示，记录如下：
（1）20袋样本总质量比标准20袋总质量多还是少？多或少多少？
（2）若标准标明要求是450±2g为合格，则抽样检测的合格率是多少？
| 与标准质量的差值（单位：g） | -5 | -2 | 0 | 2 | 3 | 7 |
| 袋数 | 3 | 5 | 3 | 2 | 5 | 2 |
（2）若标准标明要求是450±2g为合格，则抽样检测的合格率是多少？
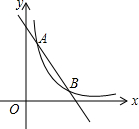如图，一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$（x＞0）的图象交于A（1，6），B（a，2）两点．
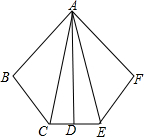如图，AB=AF，BC=FE，∠B=∠F，AD⊥CE．