题目内容
2.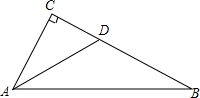 如图,在Rt△ABC中,∠C=90°,AD平分∠A,交边BC于点D,BD=2CD,求证:BC=$\sqrt{3}$•AC.
如图,在Rt△ABC中,∠C=90°,AD平分∠A,交边BC于点D,BD=2CD,求证:BC=$\sqrt{3}$•AC.
分析 作DE⊥AB于E,根据角平分线性质求出DE=CD,推出BD=2DE,根据含30°角的直角三角形的判定方法得出∠B=30°,即可得出结论.
解答 证明:作DE⊥AB于E,如图所示:
则∠DEB=90°,
∵∠C=90°,AD平分∠BAC,DE⊥AB,
∴DE=CD,
∵BD=2CD,
∴BD=2DE,
∴∠B=30°,
∴BC=$\sqrt{3}$•AC.
点评 本题考查了含30°角直角三角形性质,角平分线性质的应用;通过作辅助线根据角平分线的性质求出BD=2DE是解此题的关键.

练习册系列答案
相关题目
12. 如图,长方形内有两个相邻的正方形,面积分别为2和4,则阴影部分的面积为( )
如图,长方形内有两个相邻的正方形,面积分别为2和4,则阴影部分的面积为( )
 如图,长方形内有两个相邻的正方形,面积分别为2和4,则阴影部分的面积为( )
如图,长方形内有两个相邻的正方形,面积分别为2和4,则阴影部分的面积为( )| A. | $2\sqrt{2}-2$ | B. | $2\sqrt{2}+2$ | C. | 2 | D. | $1+\sqrt{2}$ |
12.下列说法正确的是( )
| A. | 0、b、3(a-b)都是单项式 | B. | 单项式a没有次数 | ||
| C. | $\frac{1}{x}$是代数式 | D. | x2-2xy-y是由x2、2xy、y2三项组成 |
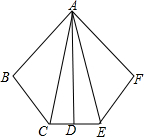 如图,AB=AF,BC=FE,∠B=∠F,AD⊥CE.
如图,AB=AF,BC=FE,∠B=∠F,AD⊥CE.