题目内容
20.小强让小彬随便想一个数,并将此数乘5,加7,然后乘2,再减4,最后将结果告诉他,他只要将这个结果减10,再除以10,就能知道小彬所想的数.你知道这是为什么吗?分析 利用代数式先表示出一个数乘5,加7,然后乘2,再减4,然后再表示出这个结果减10,再除以10,最后得到结果与小彬想一个数进行比较可判断小彬所想的数.
解答 解:设小彬所想的数为x,
则{[(5x+7)×2-4]-10}×$\frac{1}{10}$=[10x+14-4-10]×$\frac{1}{10}$=x,
所以小强将这个结果减10,再除以10正好等于小彬所想的数.
点评 本题考查了列代数式:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.本题的关键是用代数式表示出小强运算后的结果数.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
12.下列说法正确的是( )
| A. | 0、b、3(a-b)都是单项式 | B. | 单项式a没有次数 | ||
| C. | $\frac{1}{x}$是代数式 | D. | x2-2xy-y是由x2、2xy、y2三项组成 |
7.下列说法中正确的是( )
| A. | 横坐标为0的点在x轴上 | |
| B. | 点M(-3,-5)到x轴的距离为-5 | |
| C. | 在平面直角坐标系内,点A(1,-4)和点B(-4,1)表示同一个点 | |
| D. | 若a=0,则点P(2,a)在x轴上 |
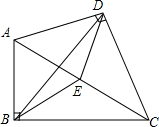 如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠ACB=29°,∠ACD=45°,E为对角线AC的中点.
如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠ACB=29°,∠ACD=45°,E为对角线AC的中点.