题目内容
18.已知m>0,n>0,且2m-$\sqrt{mn}$-5n=0,求$\frac{m-3n+\sqrt{mn}}{m+2n-2\sqrt{mn}}$的值.分析 根据m>0,n>0,且2m-$\sqrt{mn}$-5n=0,可得$\sqrt{mn}=2m-5n$,然后代入所求的式子,即可解答本题.
解答 解:∵m>0,n>0,且2m-$\sqrt{mn}$-5n=0,
∴$\sqrt{mn}=2m-5n$,
∴$\frac{m-3n+\sqrt{mn}}{m+2n-2\sqrt{mn}}$
=$\frac{m-3n+(2m-5n)}{m+2n-2(2m-5n)}$
=$\frac{3m-8n}{-3m+12n}$.
点评 本题考查二次根式的化简求值,关键是将题目中的式子变形,变为所求式子需要的条件.

练习册系列答案
相关题目
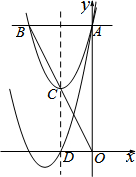 如图,抛物线y=x2+bx+8与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第二象限),抛物线的顶点C在直线OB上,且点C为OB的中点,对称轴与x轴相交于点D,平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为y=x2+6x+8.
如图,抛物线y=x2+bx+8与y轴相交于点A,与过点A平行于x轴的直线相交于点B(点B在第二象限),抛物线的顶点C在直线OB上,且点C为OB的中点,对称轴与x轴相交于点D,平移抛物线,使其经过点A、D,则平移后的抛物线的解析式为y=x2+6x+8. 如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线.若AB=2$\sqrt{3}$,则点D到AB的距离是1.
如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线.若AB=2$\sqrt{3}$,则点D到AB的距离是1.
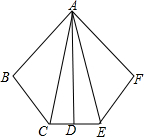 如图,AB=AF,BC=FE,∠B=∠F,AD⊥CE.
如图,AB=AF,BC=FE,∠B=∠F,AD⊥CE.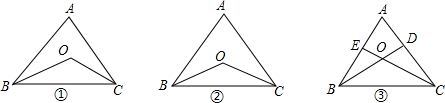
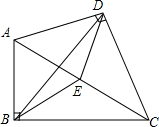 如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠ACB=29°,∠ACD=45°,E为对角线AC的中点.
如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠ACB=29°,∠ACD=45°,E为对角线AC的中点.