题目内容
9.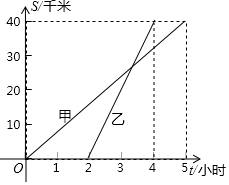 甲、乙两人沿相同的路线由A地到B地匀速前进,已知A,B两地间的距离为40千米,它们前进的路程记为s(单位:千米),甲出发后的时间记为t(单位:小时),甲、乙前进的路程与时间的函数图象如图所示,根据图象信息回答下列问题:
甲、乙两人沿相同的路线由A地到B地匀速前进,已知A,B两地间的距离为40千米,它们前进的路程记为s(单位:千米),甲出发后的时间记为t(单位:小时),甲、乙前进的路程与时间的函数图象如图所示,根据图象信息回答下列问题:(1)甲的速度是8千米/小时,乙比甲晚出发2小时;
(2)分别求出甲、乙两人前进的路程S甲、S乙与甲出发后的时间t之间的函数关系式;
(3)乙经过多长时间可以追上甲,此时两人距离B地还有多远?
分析 (1)根据速度、路程、时间之间的关系即可解决问题.
(2)利用待定系数法即可解决.
(3)利用方程组求出两个函数图象的交点的横坐标,即可求得相遇时间
解答 解:(1)甲的速度是$\frac{40}{5}$=8千米/小时,乙比甲晚出发2小时,
故答案为8,2.
(2)设S甲的解析式为s=kt,则有5k=40,k=8,
∴S=8t,
S乙与的解析式为y=mx+n,则有$\left\{\begin{array}{l}{2m+n=0}\\{4m+n=40}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=20}\\{n=-40}\end{array}\right.$,
∴s=20t-40.
(3)由$\left\{\begin{array}{l}{s=8t}\\{s=20t-40}\end{array}\right.$,解得t=$\frac{10}{3}$,
40-$\frac{80}{3}$=$\frac{40}{3}$,
∴乙经过$\frac{10}{3}$小时可以追上甲,此时两人距离B地还有$\frac{40}{3}$千米.
点评 本题考查的是一次函数的应用问题,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出函数式,再求解.

练习册系列答案
相关题目
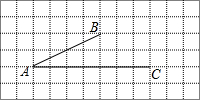 在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点都叫做格点,已知线段AB、AC的端点都在格点上.
在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点都叫做格点,已知线段AB、AC的端点都在格点上. 如图,△ABC的顶点坐标分别为A(4,4),B(2,1),C(5,1).
如图,△ABC的顶点坐标分别为A(4,4),B(2,1),C(5,1). 已知:如图,点C、D在AB上,D是AB的中点,AC=$\frac{1}{3}$AD,若CD=4,求AB的长.
已知:如图,点C、D在AB上,D是AB的中点,AC=$\frac{1}{3}$AD,若CD=4,求AB的长. 已知:如图,线段a和b
已知:如图,线段a和b