题目内容
5.某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总数排列名次,在规定时间内每人踢100个以上(含100个)为优秀,下表是成绩最好的甲、乙两班各5名学生的比赛数据.(单位:个)| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
| 乙班 | 100 | 96 | 110 | 90 | 104 | 500 |
分析 平均数=总成绩÷学生人数;中位数是按次序排列后的第3个数.根据方差的计算公式得到数据的方差.
解答 解:甲班5名学生比赛成绩的中位数是97个,乙班5名学生比赛成绩的中位数是100个;
$\overline{x}$甲=$\frac{1}{5}$×500=100(个),$\overline{x}$乙=$\frac{1}{5}$×500=100(个);
S2甲=$\frac{1}{5}$[(89-100)2+(100-100)2+(96-100)2+(118-100)2+(97-100)2]=94;
S2乙=$\frac{1}{5}$[(100-100)2+(96-100)2+(110-100)2+(90-100)2+(104-100)2]=46.4,
甲班的优秀率为:2÷5=0.4=40%,乙班的优秀率为:3÷5=0.6=60%;
乙班定为冠军.因为乙班5名学生的比赛成绩的中位数比甲班大,方差比甲班小,优秀率比甲班高,综合评定乙班踢毽子水平较好.
点评 本题考查了方差,中位数的知识,用到的知识点是:将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.平均数=总数÷个数,以及方差的算法等,需注意方差小了表示成绩稳定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.学习了一次函数、二次函数、反比例函数后,爱钻研的小敏尝试用同样的方法研究函数y=$\frac{3x+1}{x}$,从而得出以下命题:
(1)当x>0时,y的值随着x的增大而减小;
(2)y的值有可能等于3;
(3)当x>0时,y的值随着x的增大越来越接近3;
(4)当y>0时,x>0或x<-$\frac{1}{3}$.
你认为真命题是( )
(1)当x>0时,y的值随着x的增大而减小;
(2)y的值有可能等于3;
(3)当x>0时,y的值随着x的增大越来越接近3;
(4)当y>0时,x>0或x<-$\frac{1}{3}$.
你认为真命题是( )
| A. | (1)(3) | B. | (1)(4) | C. | (1)(3)(4) | D. | (2)(3)(4) |
13.下列运算正确的是( )
| A. | x3÷x=x3 | B. | x2•x3=x6 | C. | (x3)2=x5 | D. | (2x)3=8x3 |
20.使分式$\frac{4}{x-2}$有意义的x的取值范围是( )
| A. | x>2 | B. | x<2 | C. | x≠2 | D. | x≥2 |
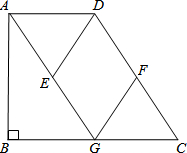 如图.在直角梯形ABCD中,AD∥BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.
如图.在直角梯形ABCD中,AD∥BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.