题目内容
14.观察下列数据:-$\frac{5}{4}$,$\frac{7}{9}$,-$\frac{9}{16}$,$\frac{11}{25}$…它们是按一定规律排列的,依照此规律,第19个数据是-$\frac{41}{400}$.分析 首先判断出每个数的正负,然后根据每个数的分子分别是5、7、9、11、…,判断出第n个数的分子是多少;最后根据每个数的分母分别是4、9、16、25、…,判断出第n个数的分母是多少,进而判断出这组数的第n个数是多少,再把n=19代入,求出第19个数数据为多少即可.
解答 解:∵这组数分别是负数、正数、负数、正数、…,
∴这组数的第n个数的正负即(-1)n的正负;
∵5=2×1+3,7=2×2+3,9=2×3+3,11=2×4+3,
∴第n个数的分子是:2n+3;
∵4=(1+1)2,9=(2+1)2,16=(3+1)2,25=(4+1)2,
∴第n个数的分母是:(n+1)2;
∴这组数的第n个数是:
(-1)n•$\frac{2n+3}{{(n+1)}^{2}}$
∴第19个数据是:
(-1)19•$\frac{2×19+3}{{(19+1)}^{2}}$=-$\frac{41}{400}$.
故答案为:-$\frac{41}{400}$.
点评 此题主要考查了探寻数列规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是求出这组数的第n个数是多少.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
4.在3.5,-0.5,0,4这四个数中,绝对值最小的一个数是( )
| A. | 3.5 | B. | -0.5 | C. | 0 | D. | 4 |
5.某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总数排列名次,在规定时间内每人踢100个以上(含100个)为优秀,下表是成绩最好的甲、乙两班各5名学生的比赛数据.(单位:个)
统计发现两班总数相等,此时有人建议,可以通过考查数据中的其他信息来评判.试从两班比赛数据的中位数、方差、优秀率三个方面考虑,你认为应该选定哪一个班为冠军?
| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
| 乙班 | 100 | 96 | 110 | 90 | 104 | 500 |
2.某校准备修建一个面积为180平方米的矩形活动场地,它的长比宽多11米,设场地的宽为x米,则可列方程为( )
| A. | x(x-11)=180 | B. | 2x+2(x-11)=180 | C. | x(x+11)=180 | D. | 2x+2(x+11)=180 |
9.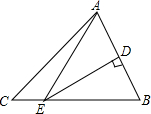 如图,在△ABC中AB的垂直平分线交AB于点D,交线段BC于点E.BC=6,AC=5,则△ACE的周长是( )
如图,在△ABC中AB的垂直平分线交AB于点D,交线段BC于点E.BC=6,AC=5,则△ACE的周长是( )
 如图,在△ABC中AB的垂直平分线交AB于点D,交线段BC于点E.BC=6,AC=5,则△ACE的周长是( )
如图,在△ABC中AB的垂直平分线交AB于点D,交线段BC于点E.BC=6,AC=5,则△ACE的周长是( )| A. | 14 | B. | 13 | C. | 12 | D. | 11 |
6.经过某十字路口的汽车,可能直行,也可能左转或者右转,如果这三种可能性大小相同,则经过这个十字路口的两辆汽车一辆左转,一辆右转的概率是( )
| A. | $\frac{4}{7}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{9}$ |
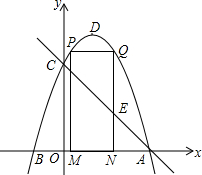 如图,直线y=-x+3与x轴、y轴分别交于A、C两点,对称轴为直线x=1的抛物线过A、C两点,抛物线与x轴的另一个交点为点B(B在A的左侧),顶点为D.
如图,直线y=-x+3与x轴、y轴分别交于A、C两点,对称轴为直线x=1的抛物线过A、C两点,抛物线与x轴的另一个交点为点B(B在A的左侧),顶点为D.