题目内容
如图1,直角坐标系中,A点是第二象限内一点,AB⊥x轴于B,且C(0,2)是y轴正半轴上一点,OB-OC=2,S四边形ABOC=11.
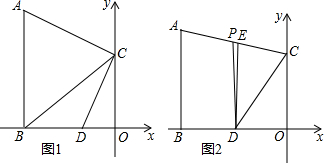
(1)求A点坐标;
(2)设D为线段OB上一动点,当∠COE=∠A时,CD与AC之间存在怎样的位置关系,并证明;
(3)当D点在线段OB上运动时,连接AD、CD,如图2,DE平分∠ADC,DP∥AB.则以下两个结论:
①∠PDE的大小不变;
②
的大小不变.
其中只有一个结论是正确的,请你判断哪个结论正确并说明理由.

(1)求A点坐标;
(2)设D为线段OB上一动点,当∠COE=∠A时,CD与AC之间存在怎样的位置关系,并证明;
(3)当D点在线段OB上运动时,连接AD、CD,如图2,DE平分∠ADC,DP∥AB.则以下两个结论:
①∠PDE的大小不变;
②
| |∠OCD-∠BAD| |
| ∠PDE |
其中只有一个结论是正确的,请你判断哪个结论正确并说明理由.
考点:坐标与图形性质,平行线的性质,三角形的面积,三角形内角和定理,三角形的外角性质
专题:探究型
分析:(1)理由C点坐标得到OB=2+OC=4,则B点坐标为(-4,0),设A点坐标为(-4,b),根据梯形的面积公式得到
(2+b)•4=11,解得b=
,则A点坐标为(-4,
);
(2)作CH⊥AB于H,如图1,证明Rt△OCD∽Rt△HCA,理由相似比即可得到
=
=
=
;
(3)如图2,由PD∥AB得到PD∥AB∥OC,根据平行线的性质得∠PDA=∠BAD,∠PDC=∠OCD,则∠ADC=∠BAD+∠OCD,再利用角平分线的性质得∠EDC=
∠ADC=
(∠BAD+∠OCD),所以∠PDE=|∠PDC-∠EDC|=|∠OCD-
(∠BAD+∠OCD)|=
|∠OCD-∠BAD|,则有
=2.
| 1 |
| 2 |
| 7 |
| 2 |
| 7 |
| 2 |
(2)作CH⊥AB于H,如图1,证明Rt△OCD∽Rt△HCA,理由相似比即可得到
| CD |
| AC |
| OC |
| CH |
| 2 |
| 4 |
| 1 |
| 2 |
(3)如图2,由PD∥AB得到PD∥AB∥OC,根据平行线的性质得∠PDA=∠BAD,∠PDC=∠OCD,则∠ADC=∠BAD+∠OCD,再利用角平分线的性质得∠EDC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| |∠OCD-∠BAD| |
| ∠PDE |
解答: 解:(1)∵C(0,2),OB-OC=2,
解:(1)∵C(0,2),OB-OC=2,
∵OB=2+OC=2+2=4,
∴B点坐标为(-4,0),
设A点坐标为(-4,b),
∴
(2+b)•4=11,解得b=
,
∴A点坐标为(-4,
);
(2)CD=
AC.理由如下:
作CH⊥AB于H,如图1,
∴∠CDO=∠A,
∴Rt△OCD∽Rt△HCA,
∴
=
=
,
即CD=
AC;
(3)结论②正确.理由如下:
如图2,∵PD∥AB,
∴PD∥AB∥OC,
∴∠PDA=∠BAD,∠PDC=∠OCD,
∴∠ADC=∠PDA+∠PDC=∠BAD+∠OCD,
∵DE平分∠ADC,
∴∠EDC=
∠ADC=
(∠BAD+∠OCD),
∴∠PDE=|∠PDC-∠EDC|=|∠OCD-
(∠BAD+∠OCD)|=
|∠OCD-∠BAD|,
∴
=2.
 解:(1)∵C(0,2),OB-OC=2,
解:(1)∵C(0,2),OB-OC=2,∵OB=2+OC=2+2=4,
∴B点坐标为(-4,0),
设A点坐标为(-4,b),
∴
| 1 |
| 2 |
| 7 |
| 2 |
∴A点坐标为(-4,
| 7 |
| 2 |
(2)CD=
| 1 |
| 2 |
作CH⊥AB于H,如图1,
∴∠CDO=∠A,
∴Rt△OCD∽Rt△HCA,
∴
| CD |
| AC |
| OC |
| CH |
| 2 |
| 4 |
即CD=
| 1 |
| 2 |
(3)结论②正确.理由如下:
如图2,∵PD∥AB,
∴PD∥AB∥OC,
∴∠PDA=∠BAD,∠PDC=∠OCD,
∴∠ADC=∠PDA+∠PDC=∠BAD+∠OCD,
∵DE平分∠ADC,
∴∠EDC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠PDE=|∠PDC-∠EDC|=|∠OCD-
| 1 |
| 2 |
| 1 |
| 2 |
∴
| |∠OCD-∠BAD| |
| ∠PDE |
点评:本题考查了坐标与图形性质:利用点的坐标求线段的长和判断线段与坐标轴的位置关系.也考查了相似的判定与性质和平行线的性质.

练习册系列答案
相关题目
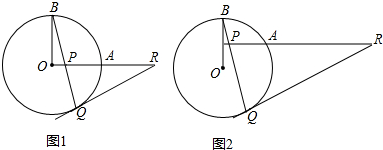
 (1)如图1、图2,点P是⊙O外一点,作直线OP,交⊙O于点M、N,则有结论:①点M是点P到⊙O的最近点;②点N是点P到⊙O的最远点.
(1)如图1、图2,点P是⊙O外一点,作直线OP,交⊙O于点M、N,则有结论:①点M是点P到⊙O的最近点;②点N是点P到⊙O的最远点.
 如图:△ABC中,∠ABC和∠ACB的平分线交于F点,过F点作DE∥BC,分别交AB、AC于点D、E.
如图:△ABC中,∠ABC和∠ACB的平分线交于F点,过F点作DE∥BC,分别交AB、AC于点D、E.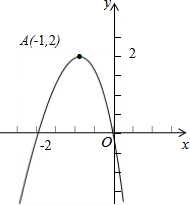 (1)请写出图中所示的二次函数图象的解析式;
(1)请写出图中所示的二次函数图象的解析式; 如图,在△ABC中,边AB、AC的垂直平分线分别交BC于E、F.
如图,在△ABC中,边AB、AC的垂直平分线分别交BC于E、F.