题目内容
如图1,已知OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合)BP的延长线交⊙O于Q,过Q点作⊙O的切线交OA的延长线于R.
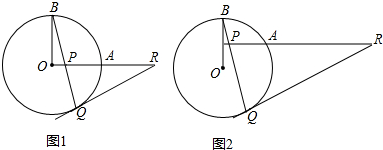
(1)证明:RP=RQ.
(2)请探究下列变化:
A、变化一:交换题设与结论.已知:如图1,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,R是OA的延长线上一点,且RP=RQ.证明:RQ为⊙O的切线.
B、变化二:运动探求.(1)如图2,若OA向上平移,变化一中结论还成立吗?(只交待判断)
答: .

(1)证明:RP=RQ.
(2)请探究下列变化:
A、变化一:交换题设与结论.已知:如图1,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,R是OA的延长线上一点,且RP=RQ.证明:RQ为⊙O的切线.
B、变化二:运动探求.(1)如图2,若OA向上平移,变化一中结论还成立吗?(只交待判断)
答:
考点:圆的综合题
专题:
分析:(1)连接OQ,利用RQ为⊙O的切线,得出∠OQB+∠PQR=90°,根据半径OB=OQ及OA⊥OB,得出∠OQB=∠OBQ,∠OBQ+∠BPO=90°,从而得∠PQR=∠QPR,证明结论;
(2)A,变化一的证明:与原命题的证明过程相反,由RP=RQ,可知∠PQR=∠QPR=∠BPO,再利用互余关系将角进行转化,证明∠OQB+∠PQR=90°,即∠OQR=90°即可;
B,成立,变化二的证明:仿照原命题的证明方法进行即可.
(2)A,变化一的证明:与原命题的证明过程相反,由RP=RQ,可知∠PQR=∠QPR=∠BPO,再利用互余关系将角进行转化,证明∠OQB+∠PQR=90°,即∠OQR=90°即可;
B,成立,变化二的证明:仿照原命题的证明方法进行即可.
解答:(1)证明:连接OQ,
∵RQ为⊙O的切线,
∴∠OQR=∠OQB+∠PQR=90°,
又∵OB=OQ,OA⊥OB,
∴∠OQB=∠OBQ,∠OBQ+∠BPO=90°,
∴∠PQR=∠BPO,
而∠BPO=∠QPR,
∴∠PQR=∠QPR,
∴RP=RQ;
(2)A,变化一:
证明:∵RP=RQ,
∴∠PQR=∠QPR=∠BPO,
又∵OB=OQ,OA⊥OB,
∴∠OQB=∠OBQ,∠OBQ+∠BPO=90°,
∴∠OQB+∠PQR=90°,即∠OQR=90°,
∴RQ为⊙O的切线;
B,变化二.若OA向上平移,变化一中的结论还成立,
理由如下同A,
故答案为:成立.
∵RQ为⊙O的切线,
∴∠OQR=∠OQB+∠PQR=90°,
又∵OB=OQ,OA⊥OB,
∴∠OQB=∠OBQ,∠OBQ+∠BPO=90°,

∴∠PQR=∠BPO,
而∠BPO=∠QPR,
∴∠PQR=∠QPR,
∴RP=RQ;
(2)A,变化一:
证明:∵RP=RQ,
∴∠PQR=∠QPR=∠BPO,
又∵OB=OQ,OA⊥OB,
∴∠OQB=∠OBQ,∠OBQ+∠BPO=90°,
∴∠OQB+∠PQR=90°,即∠OQR=90°,
∴RQ为⊙O的切线;
B,变化二.若OA向上平移,变化一中的结论还成立,
理由如下同A,
故答案为:成立.
点评:此题考查了切线的性质、等腰三角形的性质以及垂直的定义.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
随着微电子制造技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占为7×10-7平方毫米,这个数用小数表示为( )
| A、0.000007 |
| B、0.000070 |
| C、0.0000700 |
| D、0.0000007 |