题目内容
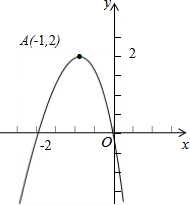 (1)请写出图中所示的二次函数图象的解析式;
(1)请写出图中所示的二次函数图象的解析式;(2)若-3≤x≤3,该函数的最大值、最小值分别为
考点:待定系数法求二次函数解析式,二次函数的最值
专题:计算题
分析:(1)由于已知抛物线与x轴的两交点坐标,则可设交点式y=ax(x+2),然后把A点坐标代入即可得到a的值,从而得到抛物线解析式;
(2)根据二次函数的性质当-3≤x≤3时,x=-1时,函数有最大值2;当x=3时,函数有最小值,把x=3代入解析式计算函数的最小值.
(2)根据二次函数的性质当-3≤x≤3时,x=-1时,函数有最大值2;当x=3时,函数有最小值,把x=3代入解析式计算函数的最小值.
解答:解:(1)设抛物线解析式为y=ax(x+2),
把A(-1,2)代入得a•(-1)•(-1+2)=2,解得a=-2,
所以抛物线解析式为y=-2x(x+2)=-2x2-4x;
(2)抛物线y=2x2+4x的开口向下,对称轴为直线x=-1,
当-3≤x≤3时,x=-1时,函数有最大值2;当x=3时,函数有最小值为y=-2×9-4×3=-30.
故答案为2,-30.
把A(-1,2)代入得a•(-1)•(-1+2)=2,解得a=-2,
所以抛物线解析式为y=-2x(x+2)=-2x2-4x;
(2)抛物线y=2x2+4x的开口向下,对称轴为直线x=-1,
当-3≤x≤3时,x=-1时,函数有最大值2;当x=3时,函数有最小值为y=-2×9-4×3=-30.
故答案为2,-30.
点评:本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
 如图,a,b,c是数轴上三个点A、B、C所对应的实数.试化简:
如图,a,b,c是数轴上三个点A、B、C所对应的实数.试化简: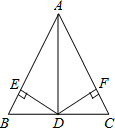 如图,在△ABC中,AB=AC,D为BC上一点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,
如图,在△ABC中,AB=AC,D为BC上一点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,