题目内容
 如图:△ABC中,∠ABC和∠ACB的平分线交于F点,过F点作DE∥BC,分别交AB、AC于点D、E.
如图:△ABC中,∠ABC和∠ACB的平分线交于F点,过F点作DE∥BC,分别交AB、AC于点D、E.(1)图中有几个等腰三角形?请写出来;
(2)求证:DE=BD+CE.
考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:(1)根据角平分线的性质,可得∠ABF与∠FBC的关系,∠ACF与∠FCB的关系,根据平行线的性质,可得∠FBC与∠BFD的关系,∠FCB与∠EFC的关系,根据等腰三角形的判定,可得答案;
(2)根据等量代换,可得答案.
(2)根据等量代换,可得答案.
解答:(1)解:图中有2个等腰三角形:等腰三角形△DBF,等腰三角形△EFC;
(2)证明:∵∠ABC和∠ACB的平分线交于F点,
∴∠ABF=∠FBC,∠ACF=∠FCB.
∵DE∥BC,
∴∠FBC=∠BFD,∠FCB=∠EFC,
∴∠DBF=∠DFB,∠ECF=∠EFC,
∴DB=DF,EC=EF.
∵DE=DF+EF,
∴DE=BD+CE.
(2)证明:∵∠ABC和∠ACB的平分线交于F点,
∴∠ABF=∠FBC,∠ACF=∠FCB.
∵DE∥BC,
∴∠FBC=∠BFD,∠FCB=∠EFC,
∴∠DBF=∠DFB,∠ECF=∠EFC,
∴DB=DF,EC=EF.
∵DE=DF+EF,
∴DE=BD+CE.
点评:本题考查了等腰三角形的判定与性质,利用了等腰三角形的判定与性质.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
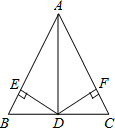 如图,在△ABC中,AB=AC,D为BC上一点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,
如图,在△ABC中,AB=AC,D为BC上一点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,