题目内容
11.等腰梯形的腰长是12厘米,一对角线分中位线成4厘米和10厘米,则此对角线长为4$\sqrt{19}$厘米.分析 作DH⊥BC于H,根据三角形中位线定理求出AD、BC,根据勾股定理计算即可.
解答 解: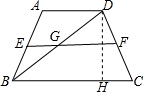 作DH⊥BC于H,
作DH⊥BC于H,
∵EF是梯形ABCD的中位线,
∴EG、GF分别是△ABD和△DBC的中位线,
∴AD=2EG=8厘米,BC=2GF=20厘米,
∴CH=(20-8)÷2=6厘米,BH=14厘米,
∴DH=$\sqrt{C{D}^{2}-C{H}^{2}}=6\sqrt{3}$厘米,
∴BD=$\sqrt{B{H}^{2}+D{H}^{2}}$=4$\sqrt{19}$厘米,
故答案为:4$\sqrt{19}$.
点评 本题考查的是梯形的中位线定理和等腰梯形的性质的应用,掌握三角形的中位线定理、梯形的中位线定理是解题的关键,注意勾股定理的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.n边形的对角线的总条数为m,则m=$\frac{n(n-3)}{2}$,其中自变量n的取值范围是( )
| A. | 全体实数 | B. | 全体整数 | ||
| C. | n≥3 | D. | 大于或等于3的整数 |
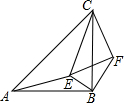 如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
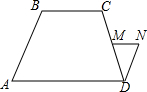 如图,在梯形ABCD中,AD∥BC,M是CD中点,MN∥AD,DN∥AB,设BC=a,AD=b(a<b),那么MN与a、b有怎样的数量关系.试加以证明.
如图,在梯形ABCD中,AD∥BC,M是CD中点,MN∥AD,DN∥AB,设BC=a,AD=b(a<b),那么MN与a、b有怎样的数量关系.试加以证明. 实数a,b,c,d在数轴上的位置如图所示,|a|=|b|,化简:|b-a|-3|a+c|-|-b-c|+|d-c|.
实数a,b,c,d在数轴上的位置如图所示,|a|=|b|,化简:|b-a|-3|a+c|-|-b-c|+|d-c|.