Question

5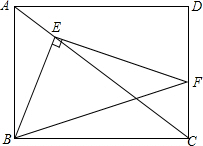．如图所示，矩形ABCD的边AB=3，Rt△BEF的直角顶点E在对角线AC上，另一顶点F在边CD上，若△BEF的一个锐角为30°，则BC的长为3$\sqrt{3}$或$\sqrt{3}$．

Answer 1

分析 由矩形的性质和已知条件证出B、C、F、E四点共圆，由圆周角定理得出∠BFE=∠ACB，分两种情况：①当∠BFE=30°时，∠ACB=30°；
②当∠EBF=30°时，∠ACB=∠BFE=60°；由三角函数分别求出BC即可．

解答 解：∵四边形ABCD是矩形，
∴∠BCD=90°，
∵∠BEF=90°，
∴∠BCD+∠BEF=180°，
∴B、C、F、E四点共圆，
∴∠BFE=∠ACB，
分两种情况：①当∠BFE=30°时，∠ACB=30°，
∴BC=$\sqrt{3}$AB=3$\sqrt{3}$；
②当∠EBF=30°时，∠ACB=∠BFE=60°，
BC=$\frac{AB}{\sqrt{3}}$=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$；
综上所述：BC的长为3$\sqrt{3}$或$\sqrt{3}$；
故答案为：3$\sqrt{3}$或$\sqrt{3}$．

点评 本题考查了矩形的性质、四点共圆、圆周角定理、三角函数等知识；熟练掌握矩形的性质，证明四点共圆是解决问题的关键．