题目内容
11.将函数y=x2-2x-3图象沿y轴翻折后,与原图象合起来,构成一个新函数的图象,若直线y=x+m与新图象有四个公共点,则m的取值范围为m>-$\frac{13}{4}$且m≠-3.分析 先根据函数解析式画出图形,然后结合图形可求得取值范围.
解答 解:翻折后所得新图象如图所示.
∵函数y=x2-2x-3=(x-1)2-4,
∴顶点P的坐标为(1,-4),
∴Q(-1,-4),
当直线y=x+m经过Q(-1,-4)时,-4=-1+m,
解得m=-3,∴此时直线与新图象有3个交点,且经过点(0,-3),
∵翻折后的抛物线y=(x+1)2-4,
由$\left\{\begin{array}{l}{y=x+m}\\{y=(x+1)^{2}-4}\end{array}\right.$消去y得x2+x-3-m=0,
当△=0时,1-4(-3-m))=0,
m=-$\frac{13}{4}$,此时直线y=x+m与新图象有3个交点
∴若直线y=x+m与新图象有四个公共点,则m的取值范围为m>-$\frac{13}{4}$且m≠-3,
故答案为m>-$\frac{13}{4}$且m≠-3.
点评 本题考查了二次函数和y轴的交点问题,平移的性质,二次函数的图象与几何变换的应用,主要考查学生的理解能力,题目比较好,有一定的难度.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
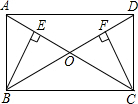 如图,矩形ABCD中,AC与BD交于O点,BE⊥AC于E,CF⊥BD于F.
如图,矩形ABCD中,AC与BD交于O点,BE⊥AC于E,CF⊥BD于F. 如图,菱形ABCD的边长为4cm,且∠ABC=120°,E是BC的中点,在BD上求点P,使PC+PE取最小值,并求这个最小值.
如图,菱形ABCD的边长为4cm,且∠ABC=120°,E是BC的中点,在BD上求点P,使PC+PE取最小值,并求这个最小值.
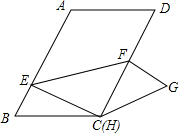 如图,在?ABCD中,AB=8,BC=6,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将?ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点H,点D的对应点为点G.
如图,在?ABCD中,AB=8,BC=6,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将?ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点H,点D的对应点为点G.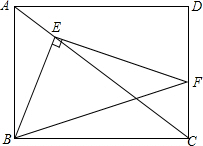 如图所示,矩形ABCD的边AB=3,Rt△BEF的直角顶点E在对角线AC上,另一顶点F在边CD上,若△BEF的一个锐角为30°,则BC的长为3$\sqrt{3}$或$\sqrt{3}$.
如图所示,矩形ABCD的边AB=3,Rt△BEF的直角顶点E在对角线AC上,另一顶点F在边CD上,若△BEF的一个锐角为30°,则BC的长为3$\sqrt{3}$或$\sqrt{3}$. 如图,锐角△ABC中,∠ABC=45°,BD是∠ABC的平分线,BC=5,E为BC上一动点,F为BD上一动点,则CF+EF的最小值为$\frac{5\sqrt{2}}{2}$.
如图,锐角△ABC中,∠ABC=45°,BD是∠ABC的平分线,BC=5,E为BC上一动点,F为BD上一动点,则CF+EF的最小值为$\frac{5\sqrt{2}}{2}$.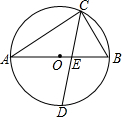 如图,AB为⊙O的直径,弦CD平分圆周角∠ACB,交AB于E,若AC=2BC,求$\frac{CE}{DE}$的值.
如图,AB为⊙O的直径,弦CD平分圆周角∠ACB,交AB于E,若AC=2BC,求$\frac{CE}{DE}$的值.