题目内容
18.课堂上,李老师提出这样一个问题:已知$\frac{x+3}{(x-2)^{2}}$=$\frac{A}{x-2}$+$\frac{B}{(x-2)^{2}}$,求整数A,B的值.小明回答了解题思路:首先对等式右边进行通分,得$\frac{A(x-2)+B}{(x-2)^{2}}$,即$\frac{Ax-2A+B}{(x-2)^{2}}$利用多项式相等,则对应的系数相等可列方程组$\left\{\begin{array}{l}{A=1}\\{-2A+B=3}\end{array}\right.$,解这个方程组即可求出整数A,B的值.
李老师肯定了小明的解题思路是正确的,请你根据上述思路解答下列问题:
已知$\frac{3x-4}{{x}^{2}-3x+2}$=$\frac{A}{x-1}$+$\frac{B}{x-2}$,求整数A、B的值.
分析 已知等式右边通分并利用同分母分式的加法法则计算,利用分式相等的条件求出A与B的值.
解答 解:已知等式整理得:$\frac{3x-4}{{x}^{2}-3x+2}$=$\frac{A(x-2)+B(x-1)}{{x}^{2}-3x+2}$,
可得3x-4=(A+B)x-2A-B,
∴$\left\{\begin{array}{l}{A+B=3}\\{2A+B=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{A=1}\\{B=2}\end{array}\right.$.
点评 此题考查了分式的加减法,弄清题中的解法是解本题的关键.

练习册系列答案
相关题目
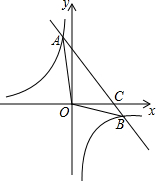 如图,已知一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-2,m)和点B(4,-2),与x轴交于点C
如图,已知一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-2,m)和点B(4,-2),与x轴交于点C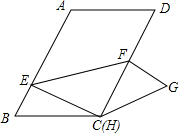 如图,在?ABCD中,AB=8,BC=6,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将?ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点H,点D的对应点为点G.
如图,在?ABCD中,AB=8,BC=6,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将?ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点H,点D的对应点为点G.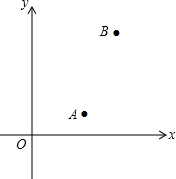 如图,已知A,B两村庄在平面直角坐标系中的坐标分别为(3,1),(5,5),若长途客车沿y轴行驶到P处时,与A,B两村庄的距离之和最小,则点P的坐标为(0,$\frac{5}{2}$).
如图,已知A,B两村庄在平面直角坐标系中的坐标分别为(3,1),(5,5),若长途客车沿y轴行驶到P处时,与A,B两村庄的距离之和最小,则点P的坐标为(0,$\frac{5}{2}$).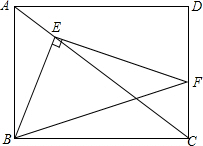 如图所示,矩形ABCD的边AB=3,Rt△BEF的直角顶点E在对角线AC上,另一顶点F在边CD上,若△BEF的一个锐角为30°,则BC的长为3$\sqrt{3}$或$\sqrt{3}$.
如图所示,矩形ABCD的边AB=3,Rt△BEF的直角顶点E在对角线AC上,另一顶点F在边CD上,若△BEF的一个锐角为30°,则BC的长为3$\sqrt{3}$或$\sqrt{3}$.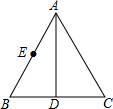 如图,已知AD是等边△ABC的角平分线,点E是AB的中点,且AD=6,BD=2$\sqrt{3}$,点M是AD上一动点,求△BEM的周长的最小值.
如图,已知AD是等边△ABC的角平分线,点E是AB的中点,且AD=6,BD=2$\sqrt{3}$,点M是AD上一动点,求△BEM的周长的最小值.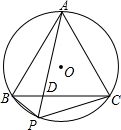 如图,P为正三角形ABC的外接圆O的劣弧BC上的任意一点,PA与BC交于D,连接PB、PC
如图,P为正三角形ABC的外接圆O的劣弧BC上的任意一点,PA与BC交于D,连接PB、PC